Bayes’ theorem in three panels
In my last post, I walked through an intuition-building visualization I created to describe mixed-effects models for a nonspecialist audience. For that presentation, I also created an analogous visualization to introduce Bayes’ Theorem, so here I will walk through that figure.
As in the earlier post, let’s start by looking at the visualization and then we will recreate it using a simpler model and smaller dataset.
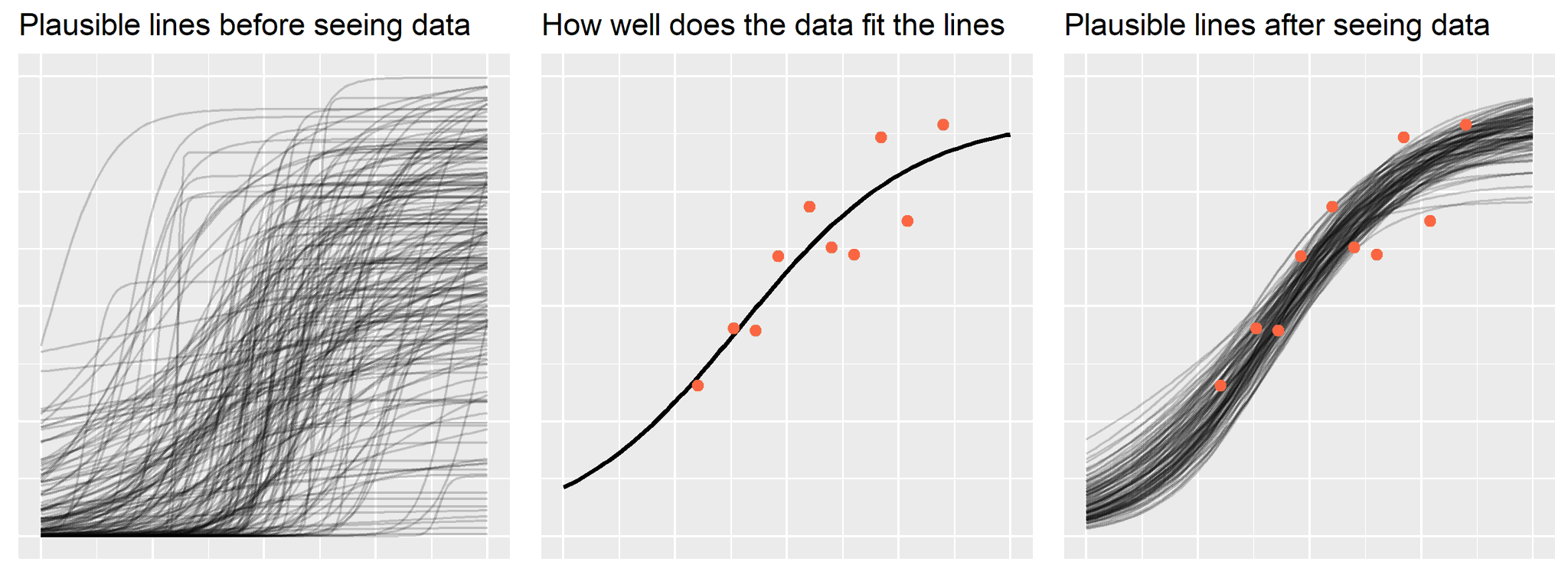
Names for things
First, let’s review the theorem. Mathematically, it says how to convert one conditional probability into another one.
\[P(B \mid A) = \frac{ P(A \mid B) * P(B)}{P(A)}\]The formula becomes more interesting in the context of statistical modeling. We have some model that describes a data-generating process and we have some observed data, but we want to estimate some unknown model parameters. In that case, the formula reads like:
\[P(\text{unknown} \mid \text{observed}) = \frac{ P(\text{observed} \mid \text{unknown}) * P(\text{unknown})}{P(\text{observed})}\]When I was first learning Bayes, this form was my anchor for remembering the formula. The goal is to learn about unknown quantity from data, so the left side needs to be “unknown given data”.
These terms have conventional names:
\[\text{posterior} = \frac{ \text{likelihood} * \text{prior}}{\text{average likelihood}}\]Prior and posterior describe when information is obtained: what we know pre-data is our prior information, and what we learn post-data is the updated information (“posterior”).
The likelihood in the equation says how likely the data is given the model parameters. I think of it as fit: How well do the parameters fit the data? Classical regression’s line of best fit is the maximum likelihood line. The likelihood also encompasses the data-generating process behind the model. For example, if we assume that the observed data is normally distributed, then we evaluate the likelihood by using the normal probability density function. You don’t need to know what that last sentence means. What’s important is that the likelihood contains our built-in assumptions about how the data is distributed.
The average likelihood—sometimes called evidence—is weird. I don’t have a script for how to describe it in an intuitive way. It’s there to make sure the math works out so that the posterior probabilities sum to 1. Some presentations of Bayes’ theorem gloss over it, noting that the posterior is proportional to the likelihood and prior information.
\[\text{updated information} \propto \text{likelihood of data} * \text{prior information}\]There it is. Update your prior information in proportion to how well it fits the observed data. My plot about Bayes’ theorem is really just this form of the equation expressed visually.
Here is an earlier post with some slides that work through these terms with some examples.

The model: nonlinear beta regression
The data I presented at the conference involved the same kinds of logistic growth curves I wrote about last year. I will use the same example dataset as in that post.
library(tidyverse)
#> ── Attaching packages ─────────────────────────────────────── tidyverse 1.3.1 ──
#> ✔ ggplot2 3.3.6 ✔ purrr 0.3.4
#> ✔ tibble 3.1.7 ✔ dplyr 1.0.9
#> ✔ tidyr 1.2.0 ✔ stringr 1.4.0
#> ✔ readr 2.1.2 ✔ forcats 0.5.1
#> ── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
#> ✖ dplyr::filter() masks stats::filter()
#> ✖ dplyr::lag() masks stats::lag()
data <- tibble(
age = c(38, 45, 52, 61, 80, 74),
prop = c(0.146, 0.241, 0.571, 0.745, 0.843, 0.738)
)
Here x is a child’s age in months and y is how intelligible the child’s speech is to strangers as a proportion. We use a nonlinear beta regression model. The beta regression handles the fact that the data are proportions, and the nonlinear piece encodes some assumptions about growth: it starts at 0, reaches some asymptote, etc. Finally, our prior information comes from our knowledge about when and how children learn to talk. (Nobody is talking in understandable sentences at 16 months of age.)
Here is the model specification. I won’t go over it in detail.
library(brms)
#> Loading required package: Rcpp
#> Loading 'brms' package (version 2.17.0). Useful instructions
#> can be found by typing help('brms'). A more detailed introduction
#> to the package is available through vignette('brms_overview').
#>
#> Attaching package: 'brms'
#> The following object is masked from 'package:stats':
#>
#> ar
inv_logit <- function(x) 1 / (1 + exp(-x))
model_formula <- bf(
# Logistic curve
prop ~ inv_logit(asymlogit) * inv(1 + exp((mid - age) * exp(scale))),
# Each term in the logistic equation gets a linear model
asymlogit ~ 1,
mid ~ 1,
scale ~ 1,
# Precision
phi ~ 1,
# This is a nonlinear Beta regression model
nl = TRUE,
family = Beta(link = identity)
)
prior_fixef <- c(
# Point of steepest growth is age 4 plus/minus 2 years
prior(normal(48, 12), nlpar = "mid", coef = "Intercept"),
prior(normal(1.25, .75), nlpar = "asymlogit", coef = "Intercept"),
prior(normal(-2, 1), nlpar = "scale", coef = "Intercept")
)
prior_phi <- c(
prior(normal(2, 1), dpar = "phi", class = "Intercept")
)
Sampling from the prior
Bayesian models are generative. They describe a data-generating process, so they can be used to simulate new observations. Richard McElreath sometimes uses the language of running a model forwards to generate new observations using parameters and running it backwards to infer the data-generating parameters from the data.
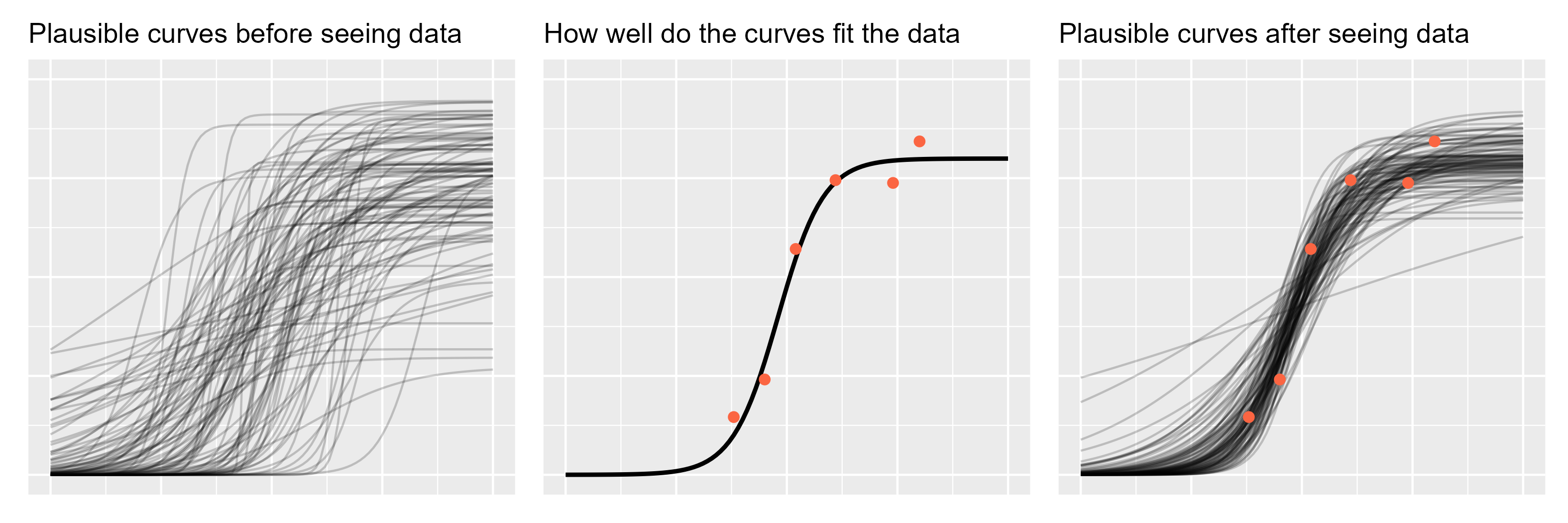
If we don’t have any data in hand, then running the model forwards will simulate data using only the prior. I am not going as far as simulating actual observations; rather I will sample regression lines from the prior. These samples represent growth trajectories that are plausible before seeing any data.
We can use sample_prior = "only" to have brms ignore the data and
sample from the prior distribution.
fit_prior <- brm(
model_formula,
data = data,
prior = c(prior_fixef, prior_phi),
iter = 2000,
chains = 4,
sample_prior = "only",
cores = 1,
control = list(adapt_delta = 0.9, max_treedepth = 15),
seed = 20211014,
file = "_caches/2020-03-04-bayes-prior",
backend = "cmdstanr",
refresh = 0
)
#> Start sampling
We can randomly draw some lines from the prior distribution by using
add_epred_draws() from the tidybayes package. An
“epred” is a predicted expectation (a model-drawn average on the same
scale as the data).
draws_prior <- data %>%
tidyr::expand(age = 0:100) %>%
tidybayes::add_epred_draws(fit_prior, ndraws = 100)
p1 <- ggplot(draws_prior) +
aes(x = age, y = .epred) +
geom_line(aes(group = .draw), alpha = .2) +
theme(
axis.ticks = element_blank(),
axis.text = element_blank(),
axis.title = element_blank()
) +
expand_limits(y = 0:1) +
ggtitle("Plausible curves before seeing data")
p1
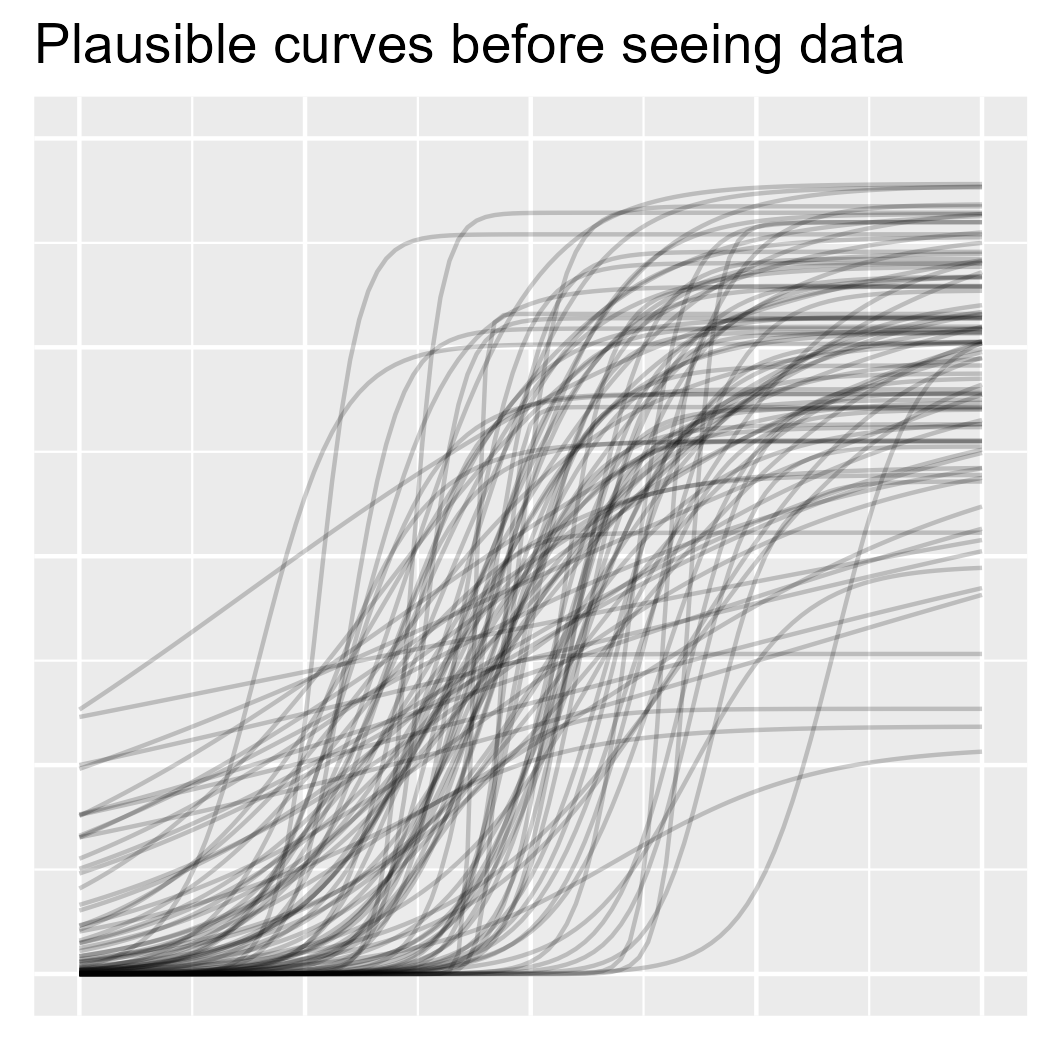
A word of encouragement! The prior is an intimidating part of Bayesian statistics. It seems highly subjective, as though we are pulling numbers from thin air, and it can be overwhelming for complex models. But if we are familiar with the kind of data we are modeling, we have prior information. We can have the model simulate new observations using the prior distribution and then plot the hypothetical data. Does anything look wrong or implausible about the simulated data? If so, then we have some prior information that we can include in our model. Note that we do not evaluate the plausibility of the simulated data based on the data we have in hand (the data we want to model); that’s not prior information.
Finding the best fit
To illustrate the likelihood, I am going to visualize a curve with a
very high likelihood. I won’t use Bayes here; instead, I will use
nonlinear least squares nls() to illustrate what a
purely data-driven fit would be. This approach is not the same as
finding the best-fitting line from the posterior
distribution1—waves hands—but hey, we’re just building
intuitions here.
# Maximum likelihood estimate
fm1 <- nls(prop ~ SSlogis(age, Asym, xmid, scal), data)
new_data <- tibble(age = 0:100) %>%
mutate(
fit = predict(fm1, newdata = .)
)
point_orange <- "#FB6542"
p2 <- ggplot(data) +
aes(x = age, y = prop) +
geom_line(aes(y = fit), data = new_data, size = 1) +
geom_point(color = point_orange, size = 2) +
theme(
axis.ticks = element_blank(),
axis.text = element_blank(),
axis.title = element_blank()
) +
expand_limits(y = 0:1) +
expand_limits(x = c(0, 100)) +
ggtitle("How well do the curves fit the data")
p2
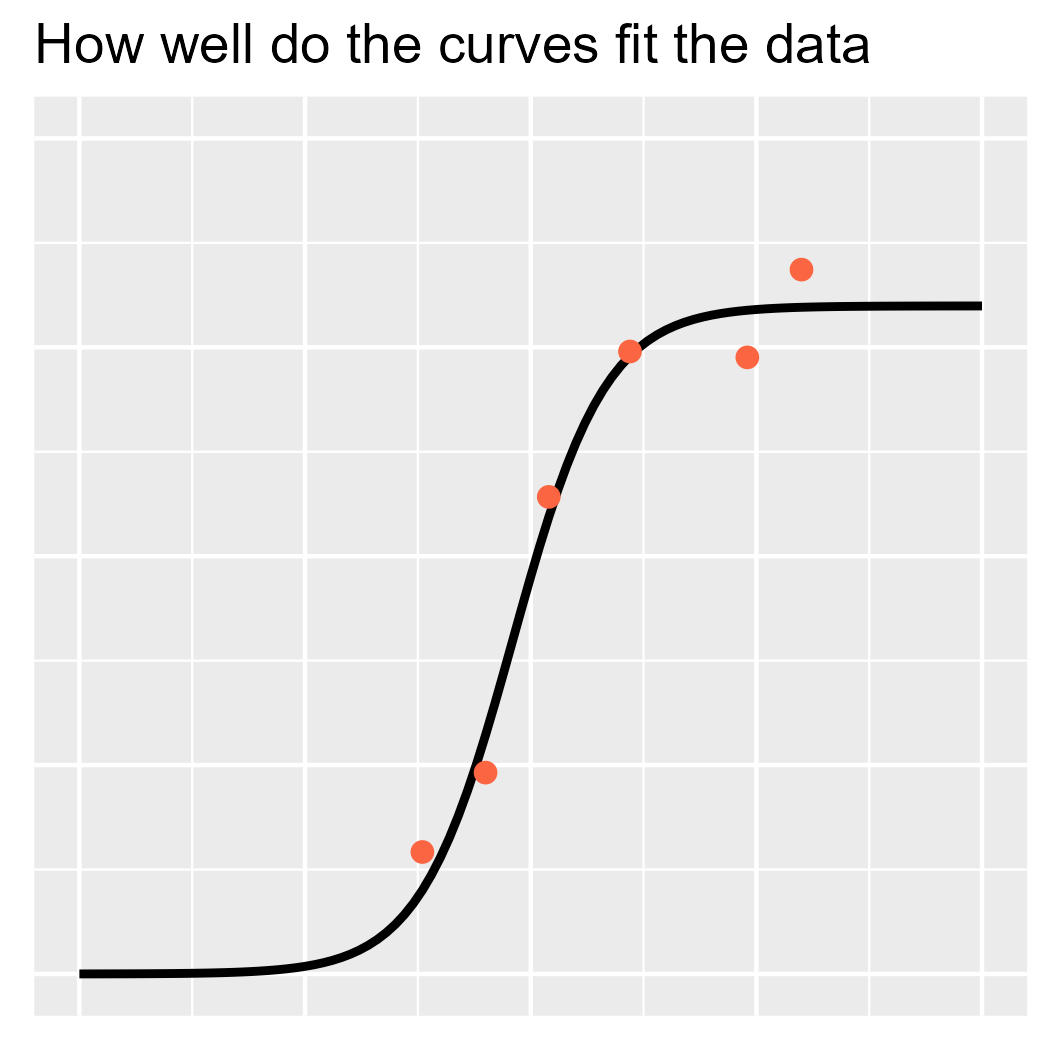
Sample from the posterior
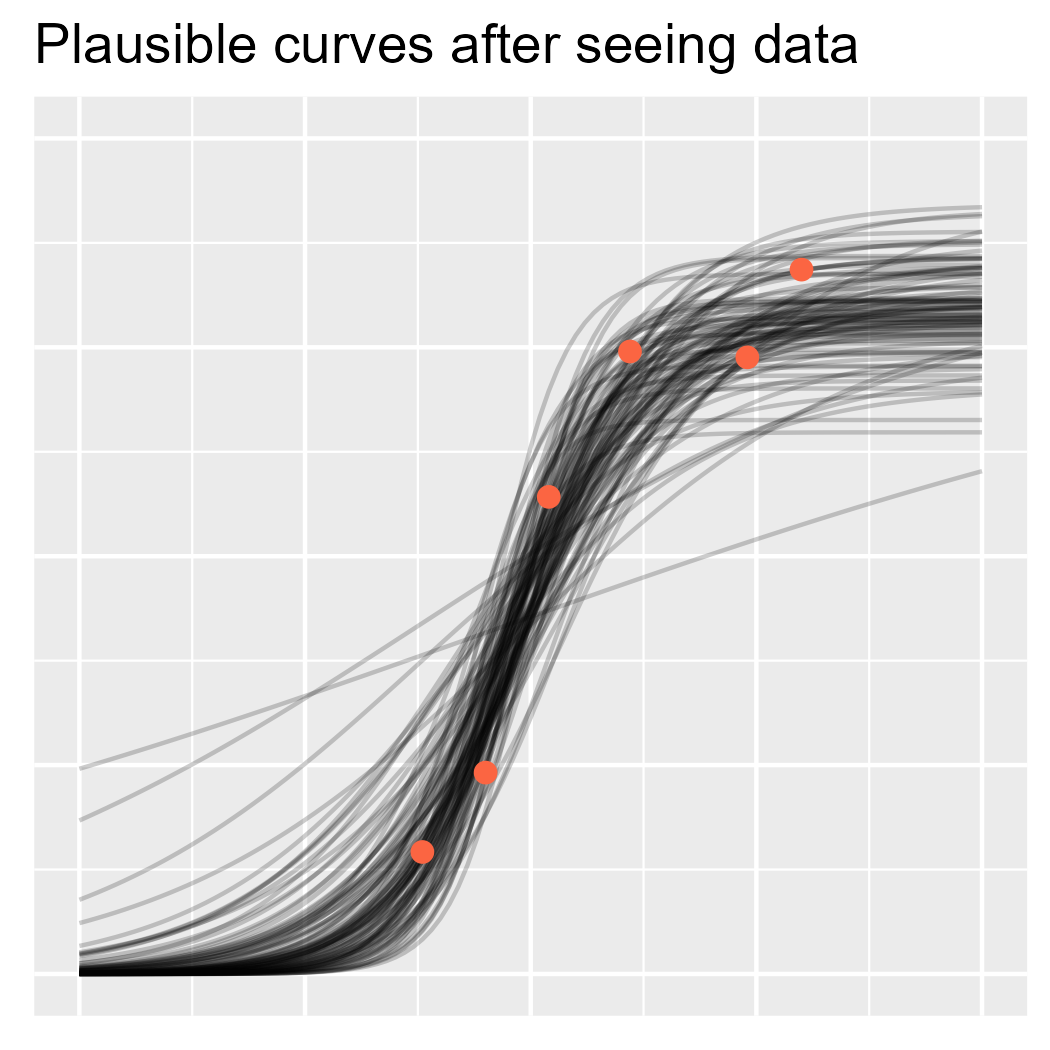
Now, let’s fit the actual model and randomly draw regression lines from the posterior distribution.
fit <- brm(
model_formula,
data = data,
prior = c(prior_fixef, prior_phi),
iter = 2000,
chains = 4,
cores = 1,
control = list(adapt_delta = 0.9, max_treedepth = 15),
seed = 20211014,
file = "_caches/2020-03-04-bayes-posterior",
backend = "cmdstanr",
refresh = 0
)
draws_posterior <- data %>%
tidyr::expand(age = 0:100) %>%
tidybayes::add_epred_draws(fit, ndraws = 100)
And now let’s plot the curves with the data, as we have data in hand now.
p3 <- ggplot(draws_posterior) +
aes(x = age, y = .epred) +
geom_line(aes(group = .draw), alpha = .2) +
geom_point(
aes(y = prop),
color = point_orange, size = 2,
data = data
) +
theme(
axis.ticks = element_blank(),
axis.text = element_blank(),
axis.title = element_blank()
) +
expand_limits(y = 0:1) +
ggtitle("Plausible curves after seeing data")
p3
Finally, we can assemble everything into one nice plot.
library(patchwork)
p1 + p2 + p3
A nice echo
3Blue1Brown is a YouTube channel that specializes in visualizing mathematical concepts. It’s amazing. About a month after my presentation, the channel covered Bayes’ theorem. The approach was more basic: It looked at probability as discrete frequency counts and using Bayes to synthesize different frequency probabilities together. Think of the familiar illness-screening puzzle: x% of positive tests are accurate, y% of the population has the illness, what is the chance of having the illness given a positive test? And yet, the video recapped Bayes’ theorem with a three-panel visualization:
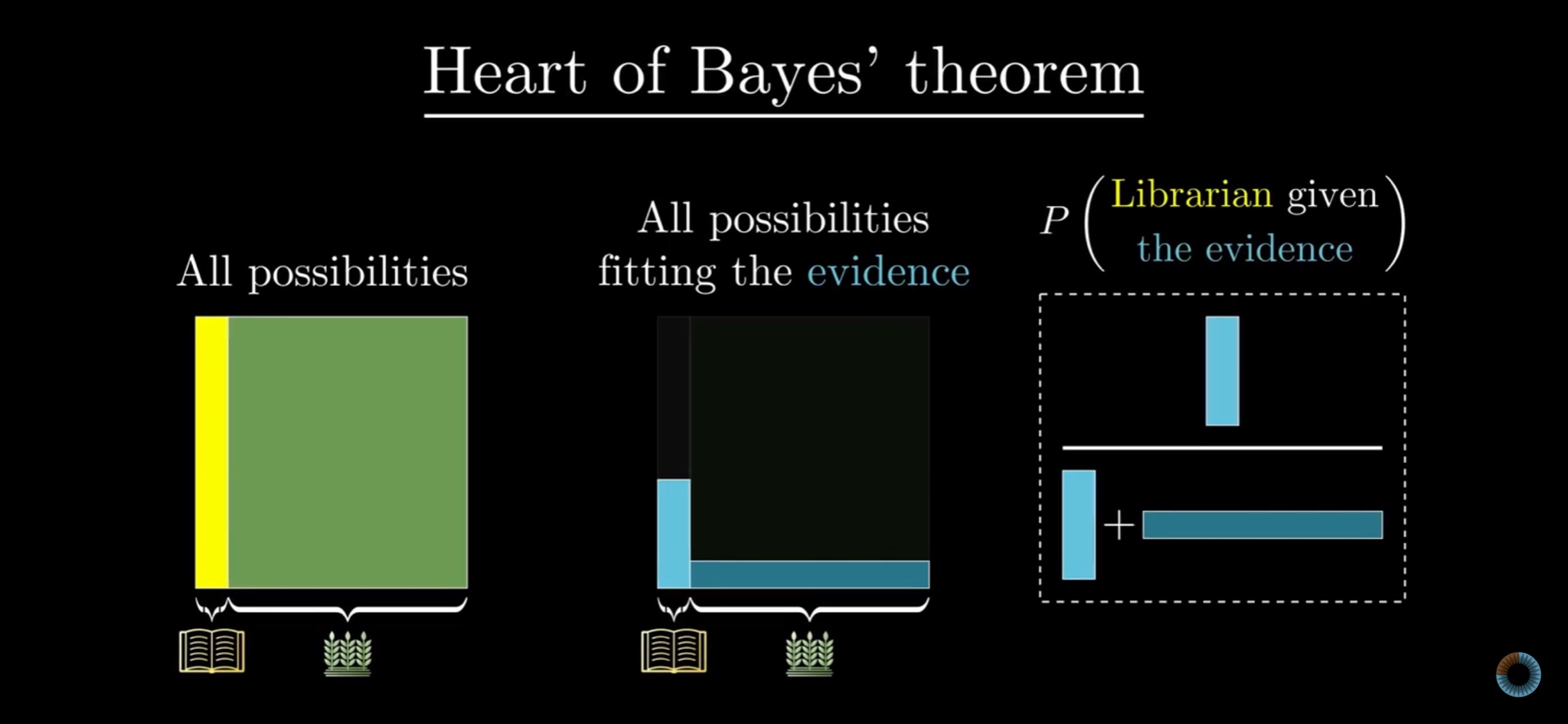
The heart of Bayes’ theorem indeed.
Last knitted on 2022-05-27. Source code on GitHub.2
-
That would be the MAP 🗺 (maximum a posteriori) estimate. ↩
-
.session_info #> ─ Session info ─────────────────────────────────────────────────────────────── #> setting value #> version R version 4.2.0 (2022-04-22 ucrt) #> os Windows 10 x64 (build 22000) #> system x86_64, mingw32 #> ui RTerm #> language (EN) #> collate English_United States.utf8 #> ctype English_United States.utf8 #> tz America/Chicago #> date 2022-05-27 #> pandoc NA #> stan (rstan) 2.21.0 #> stan (cmdstanr) 2.29.2 #> #> ─ Packages ─────────────────────────────────────────────────────────────────── #> ! package * version date (UTC) lib source #> abind 1.4-5 2016-07-21 [1] CRAN (R 4.2.0) #> arrayhelpers 1.1-0 2020-02-04 [1] CRAN (R 4.2.0) #> assertthat 0.2.1 2019-03-21 [1] CRAN (R 4.2.0) #> backports 1.4.1 2021-12-13 [1] CRAN (R 4.2.0) #> base64enc 0.1-3 2015-07-28 [1] CRAN (R 4.2.0) #> bayesplot 1.9.0 2022-03-10 [1] CRAN (R 4.2.0) #> bridgesampling 1.1-2 2021-04-16 [1] CRAN (R 4.2.0) #> brms * 2.17.0 2022-04-13 [1] CRAN (R 4.2.0) #> Brobdingnag 1.2-7 2022-02-03 [1] CRAN (R 4.2.0) #> broom 0.8.0 2022-04-13 [1] CRAN (R 4.2.0) #> cachem 1.0.6 2021-08-19 [1] CRAN (R 4.2.0) #> callr 3.7.0 2021-04-20 [1] CRAN (R 4.2.0) #> cellranger 1.1.0 2016-07-27 [1] CRAN (R 4.2.0) #> checkmate 2.1.0 2022-04-21 [1] CRAN (R 4.2.0) #> cli 3.3.0 2022-04-25 [1] CRAN (R 4.2.0) #> cmdstanr 0.5.2 2022-05-01 [1] Github (stan-dev/cmdstanr@e9c12be) #> coda 0.19-4 2020-09-30 [1] CRAN (R 4.2.0) #> codetools 0.2-18 2020-11-04 [2] CRAN (R 4.2.0) #> colorspace 2.0-3 2022-02-21 [1] CRAN (R 4.2.0) #> colourpicker 1.1.1 2021-10-04 [1] CRAN (R 4.2.0) #> crayon 1.5.1 2022-03-26 [1] CRAN (R 4.2.0) #> crosstalk 1.2.0 2021-11-04 [1] CRAN (R 4.2.0) #> data.table 1.14.2 2021-09-27 [1] CRAN (R 4.2.0) #> DBI 1.1.2 2021-12-20 [1] CRAN (R 4.2.0) #> dbplyr 2.1.1 2021-04-06 [1] CRAN (R 4.2.0) #> digest 0.6.29 2021-12-01 [1] CRAN (R 4.2.0) #> distributional 0.3.0 2022-01-05 [1] CRAN (R 4.2.0) #> downlit 0.4.0 2021-10-29 [1] CRAN (R 4.2.0) #> dplyr * 1.0.9 2022-04-28 [1] CRAN (R 4.2.0) #> DT 0.23 2022-05-10 [1] CRAN (R 4.2.0) #> dygraphs 1.1.1.6 2018-07-11 [1] CRAN (R 4.2.0) #> ellipsis 0.3.2 2021-04-29 [1] CRAN (R 4.2.0) #> emmeans 1.7.4-1 2022-05-15 [1] CRAN (R 4.2.0) #> estimability 1.3 2018-02-11 [1] CRAN (R 4.2.0) #> evaluate 0.15 2022-02-18 [1] CRAN (R 4.2.0) #> fansi 1.0.3 2022-03-24 [1] CRAN (R 4.2.0) #> farver 2.1.0 2021-02-28 [1] CRAN (R 4.2.0) #> fastmap 1.1.0 2021-01-25 [1] CRAN (R 4.2.0) #> forcats * 0.5.1 2021-01-27 [1] CRAN (R 4.2.0) #> fs 1.5.2 2021-12-08 [1] CRAN (R 4.2.0) #> generics 0.1.2 2022-01-31 [1] CRAN (R 4.2.0) #> ggdist 3.1.1 2022-02-27 [1] CRAN (R 4.2.0) #> ggplot2 * 3.3.6 2022-05-03 [1] CRAN (R 4.2.0) #> ggridges 0.5.3 2021-01-08 [1] CRAN (R 4.2.0) #> git2r 0.30.1 2022-03-16 [1] CRAN (R 4.2.0) #> glue 1.6.2 2022-02-24 [1] CRAN (R 4.2.0) #> gridExtra 2.3 2017-09-09 [1] CRAN (R 4.2.0) #> gtable 0.3.0 2019-03-25 [1] CRAN (R 4.2.0) #> gtools 3.9.2.1 2022-05-23 [1] CRAN (R 4.2.0) #> haven 2.5.0 2022-04-15 [1] CRAN (R 4.2.0) #> here 1.0.1 2020-12-13 [1] CRAN (R 4.2.0) #> highr 0.9 2021-04-16 [1] CRAN (R 4.2.0) #> hms 1.1.1 2021-09-26 [1] CRAN (R 4.2.0) #> htmltools 0.5.2 2021-08-25 [1] CRAN (R 4.2.0) #> htmlwidgets 1.5.4 2021-09-08 [1] CRAN (R 4.2.0) #> httpuv 1.6.5 2022-01-05 [1] CRAN (R 4.2.0) #> httr 1.4.3 2022-05-04 [1] CRAN (R 4.2.0) #> igraph 1.3.1 2022-04-20 [1] CRAN (R 4.2.0) #> inline 0.3.19 2021-05-31 [1] CRAN (R 4.2.0) #> jsonlite 1.8.0 2022-02-22 [1] CRAN (R 4.2.0) #> knitr * 1.39 2022-04-26 [1] CRAN (R 4.2.0) #> labeling 0.4.2 2020-10-20 [1] CRAN (R 4.2.0) #> later 1.3.0 2021-08-18 [1] CRAN (R 4.2.0) #> lattice 0.20-45 2021-09-22 [2] CRAN (R 4.2.0) #> lifecycle 1.0.1 2021-09-24 [1] CRAN (R 4.2.0) #> loo 2.5.1 2022-03-24 [1] CRAN (R 4.2.0) #> lubridate 1.8.0 2021-10-07 [1] CRAN (R 4.2.0) #> magrittr 2.0.3 2022-03-30 [1] CRAN (R 4.2.0) #> markdown 1.1 2019-08-07 [1] CRAN (R 4.2.0) #> MASS 7.3-56 2022-03-23 [2] CRAN (R 4.2.0) #> Matrix 1.4-1 2022-03-23 [2] CRAN (R 4.2.0) #> matrixStats 0.62.0 2022-04-19 [1] CRAN (R 4.2.0) #> memoise 2.0.1 2021-11-26 [1] CRAN (R 4.2.0) #> mime 0.12 2021-09-28 [1] CRAN (R 4.2.0) #> miniUI 0.1.1.1 2018-05-18 [1] CRAN (R 4.2.0) #> modelr 0.1.8 2020-05-19 [1] CRAN (R 4.2.0) #> multcomp 1.4-19 2022-04-26 [1] CRAN (R 4.2.0) #> munsell 0.5.0 2018-06-12 [1] CRAN (R 4.2.0) #> mvtnorm 1.1-3 2021-10-08 [1] CRAN (R 4.2.0) #> nlme 3.1-157 2022-03-25 [2] CRAN (R 4.2.0) #> patchwork * 1.1.1 2020-12-17 [1] CRAN (R 4.2.0) #> pillar 1.7.0 2022-02-01 [1] CRAN (R 4.2.0) #> pkgbuild 1.3.1 2021-12-20 [1] CRAN (R 4.2.0) #> pkgconfig 2.0.3 2019-09-22 [1] CRAN (R 4.2.0) #> plyr 1.8.7 2022-03-24 [1] CRAN (R 4.2.0) #> posterior 1.2.1 2022-03-07 [1] CRAN (R 4.2.0) #> prettyunits 1.1.1 2020-01-24 [1] CRAN (R 4.2.0) #> processx 3.5.3 2022-03-25 [1] CRAN (R 4.2.0) #> promises 1.2.0.1 2021-02-11 [1] CRAN (R 4.2.0) #> ps 1.7.0 2022-04-23 [1] CRAN (R 4.2.0) #> purrr * 0.3.4 2020-04-17 [1] CRAN (R 4.2.0) #> R6 2.5.1 2021-08-19 [1] CRAN (R 4.2.0) #> ragg 1.2.2 2022-02-21 [1] CRAN (R 4.2.0) #> Rcpp * 1.0.8.3 2022-03-17 [1] CRAN (R 4.2.0) #> D RcppParallel 5.1.5 2022-01-05 [1] CRAN (R 4.2.0) #> readr * 2.1.2 2022-01-30 [1] CRAN (R 4.2.0) #> readxl 1.4.0 2022-03-28 [1] CRAN (R 4.2.0) #> reprex 2.0.1 2021-08-05 [1] CRAN (R 4.2.0) #> reshape2 1.4.4 2020-04-09 [1] CRAN (R 4.2.0) #> rlang 1.0.2 2022-03-04 [1] CRAN (R 4.2.0) #> rprojroot 2.0.3 2022-04-02 [1] CRAN (R 4.2.0) #> rstan 2.21.5 2022-04-11 [1] CRAN (R 4.2.0) #> rstantools 2.2.0 2022-04-08 [1] CRAN (R 4.2.0) #> rstudioapi 0.13 2020-11-12 [1] CRAN (R 4.2.0) #> rvest 1.0.2 2021-10-16 [1] CRAN (R 4.2.0) #> sandwich 3.0-1 2021-05-18 [1] CRAN (R 4.2.0) #> scales 1.2.0 2022-04-13 [1] CRAN (R 4.2.0) #> sessioninfo 1.2.2 2021-12-06 [1] CRAN (R 4.2.0) #> shiny 1.7.1 2021-10-02 [1] CRAN (R 4.2.0) #> shinyjs 2.1.0 2021-12-23 [1] CRAN (R 4.2.0) #> shinystan 2.6.0 2022-03-03 [1] CRAN (R 4.2.0) #> shinythemes 1.2.0 2021-01-25 [1] CRAN (R 4.2.0) #> StanHeaders 2.21.0-7 2020-12-17 [1] CRAN (R 4.2.0) #> stringi 1.7.6 2021-11-29 [1] CRAN (R 4.2.0) #> stringr * 1.4.0 2019-02-10 [1] CRAN (R 4.2.0) #> survival 3.3-1 2022-03-03 [2] CRAN (R 4.2.0) #> svUnit 1.0.6 2021-04-19 [1] CRAN (R 4.2.0) #> systemfonts 1.0.4 2022-02-11 [1] CRAN (R 4.2.0) #> tensorA 0.36.2 2020-11-19 [1] CRAN (R 4.2.0) #> textshaping 0.3.6 2021-10-13 [1] CRAN (R 4.2.0) #> TH.data 1.1-1 2022-04-26 [1] CRAN (R 4.2.0) #> threejs 0.3.3 2020-01-21 [1] CRAN (R 4.2.0) #> tibble * 3.1.7 2022-05-03 [1] CRAN (R 4.2.0) #> tidybayes 3.0.2 2022-01-05 [1] CRAN (R 4.2.0) #> tidyr * 1.2.0 2022-02-01 [1] CRAN (R 4.2.0) #> tidyselect 1.1.2 2022-02-21 [1] CRAN (R 4.2.0) #> tidyverse * 1.3.1 2021-04-15 [1] CRAN (R 4.2.0) #> tzdb 0.3.0 2022-03-28 [1] CRAN (R 4.2.0) #> utf8 1.2.2 2021-07-24 [1] CRAN (R 4.2.0) #> vctrs 0.4.1 2022-04-13 [1] CRAN (R 4.2.0) #> withr 2.5.0 2022-03-03 [1] CRAN (R 4.2.0) #> xfun 0.31 2022-05-10 [1] CRAN (R 4.2.0) #> xml2 1.3.3 2021-11-30 [1] CRAN (R 4.2.0) #> xtable 1.8-4 2019-04-21 [1] CRAN (R 4.2.0) #> xts 0.12.1 2020-09-09 [1] CRAN (R 4.2.0) #> yaml 2.3.5 2022-02-21 [1] CRAN (R 4.2.0) #> zoo 1.8-10 2022-04-15 [1] CRAN (R 4.2.0) #> #> [1] C:/Users/Tristan/AppData/Local/R/win-library/4.2 #> [2] C:/Program Files/R/R-4.2.0/library #> #> D ── DLL MD5 mismatch, broken installation. #> #> ──────────────────────────────────────────────────────────────────────────────

Leave a comment