Slides from my intro to Bayesian regression talk
Back in April, I gave a guest lecture on Bayesian regression for the psychology department’s graduate statistics class. This is the same course where I first learned regression—and where I first started using R for statistics instead of for data cleaning. It was fun drawing on my experience in that course and tailoring the materials for the level of training.
Here are the materials:
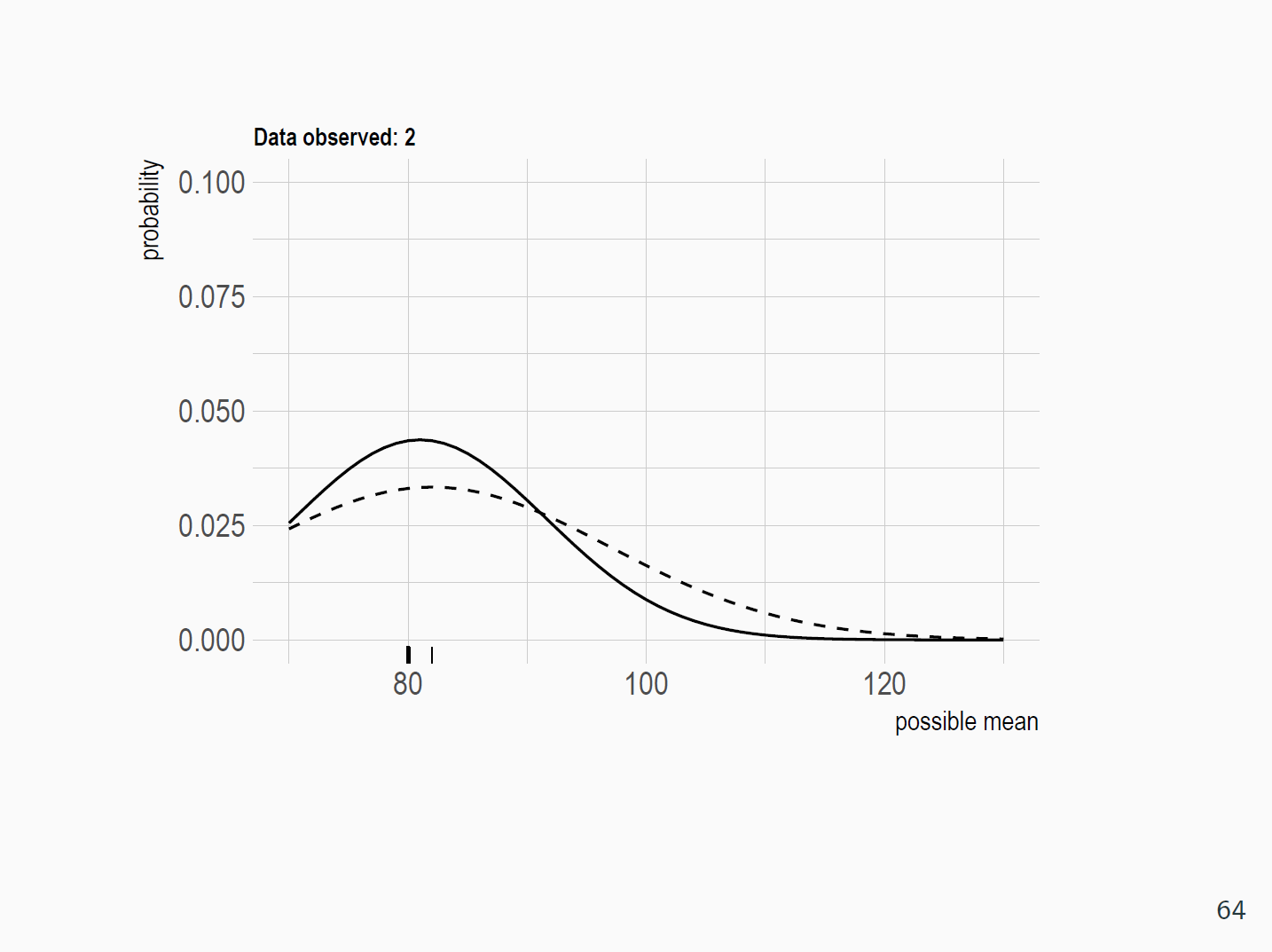
Observations (training data)
As I did with my last Bayes talk, I’m going to note some questions from the audience, so I don’t forget what kinds of questions people have when they are introduced to Bayesian statistics.
One theme was frequentist baggage 👜. One person asked about Type I and Type II error rates. I did not have a satisfactory (that is, rehearsed) answer ready for this question. I think I said something about how those terms are based on a frequentist, repeated-sampling paradigm, whereas a Bayesian approach worries about different sorts of errors. (Statistical power is still important, of course, for both approaches.) Next time, I should study up on the frequentist properties of Bayesian models, so I can field these questions better.
Other questions:
- Another bit of frequentist baggage 👜. I mentioned that with a posterior predictive distribution, we can put an uncertainty interval on any statistic we can calculate, and this point brought up the question of multiple comparisons. These are a bad thing in classical statistics. But for Bayes, there is only one model, and the multiple comparisons are really only the implications of one model.
- Someone else said that they had heard that Bayesian models can provide evidence for a null effect—how does that work? I briefly described the ROPE approach, ignoring the existence of Bayes factors entirely.
For future iterations of this tutorial, I should have a worked example, maybe a blog post, on each of these issues.
It’s kind of amusing now that I think about it. A big part of my enthusiasm for Bayesian statistics is that I find it much more intuitive than frequentist statistics. Yes! I thought to myself. I never have to worry about what the hell a confidence interval is ever again! Well, actually—no. I need to know this stuff even more thoroughly than ever if I am going to talk fluently about what makes Bayes different. ¯\_(ツ)_/¯
Last knitted on 2021-11-16. Source code on GitHub.1
-
sessioninfo::session_info() #> - Session info -------------------------------------------------------------- #> hash: flag: Clipperton Island, basketball, grimacing face #> #> setting value #> version R version 4.1.2 (2021-11-01) #> os Windows 10 x64 (build 22000) #> system x86_64, mingw32 #> ui RTerm #> language (EN) #> collate English_United States.1252 #> ctype English_United States.1252 #> tz America/Chicago #> date 2021-11-16 #> pandoc NA #> #> - Packages ------------------------------------------------------------------- #> package * version date (UTC) lib source #> assertthat 0.2.1 2019-03-21 [1] CRAN (R 4.1.0) #> cli 3.1.0 2021-10-27 [1] CRAN (R 4.1.1) #> crayon 1.4.2 2021-10-29 [1] CRAN (R 4.1.1) #> emo 0.0.0.9000 2021-10-14 [1] Github (hadley/emo@3f03b11) #> evaluate 0.14 2019-05-28 [1] CRAN (R 4.1.0) #> generics 0.1.1 2021-10-25 [1] CRAN (R 4.1.1) #> git2r 0.28.0 2021-01-10 [1] CRAN (R 4.1.1) #> glue 1.4.2 2020-08-27 [1] CRAN (R 4.1.1) #> here 1.0.1 2020-12-13 [1] CRAN (R 4.1.0) #> knitr * 1.36 2021-09-29 [1] CRAN (R 4.1.1) #> lubridate 1.8.0 2021-10-07 [1] CRAN (R 4.1.1) #> magrittr 2.0.1 2020-11-17 [1] CRAN (R 4.1.0) #> purrr 0.3.4 2020-04-17 [1] CRAN (R 4.1.0) #> ragg 1.2.0 2021-10-30 [1] CRAN (R 4.1.1) #> rlang 0.4.12 2021-10-18 [1] CRAN (R 4.1.1) #> rprojroot 2.0.2 2020-11-15 [1] CRAN (R 4.1.0) #> rstudioapi 0.13 2020-11-12 [1] CRAN (R 4.1.0) #> sessioninfo 1.2.1 2021-11-02 [1] CRAN (R 4.1.2) #> stringi 1.7.5 2021-10-04 [1] CRAN (R 4.1.1) #> stringr 1.4.0 2019-02-10 [1] CRAN (R 4.1.0) #> systemfonts 1.0.3 2021-10-13 [1] CRAN (R 4.1.1) #> textshaping 0.3.6 2021-10-13 [1] CRAN (R 4.1.1) #> xfun 0.27 2021-10-18 [1] CRAN (R 4.1.1) #> #> [1] C:/Users/trist/Documents/R/win-library/4.1 #> [2] C:/Program Files/R/R-4.1.2/library #> #> ------------------------------------------------------------------------------
Leave a comment