ICC Bot comes online
I am happy to announce the release of ICC Bot, an app for computing interrater reliability scores using the intraclass correlation coefficient (ICC).
The ICC statistic appears in repeated measures or multilevel modeling literature as a way to quantify the similarity (correlation) of data within measurement units (intra classes). In a multilevel model example, the ICC might estimate the similarity of test scores within classrooms (as opposed to between classrooms). For interrater reliability checks, the ICC estimates how similar raters’ scores are within each participant (hence, between raters). The ICC ranges from 0 to 1, and it is usually interpreted as the proportion of variance explained by between-participant differences.
\[\operatorname{ICC} = \frac{\text{between-participant variation}}{\text{between-participant variation} + \text{within-participant variation}}\]A score of 1 means that all of the variation in the scores is due to differences between the participants; a score of 0 means that none of the variation is due to differences between participants: The raters might as well have been scoring completely different participants.
Using the app
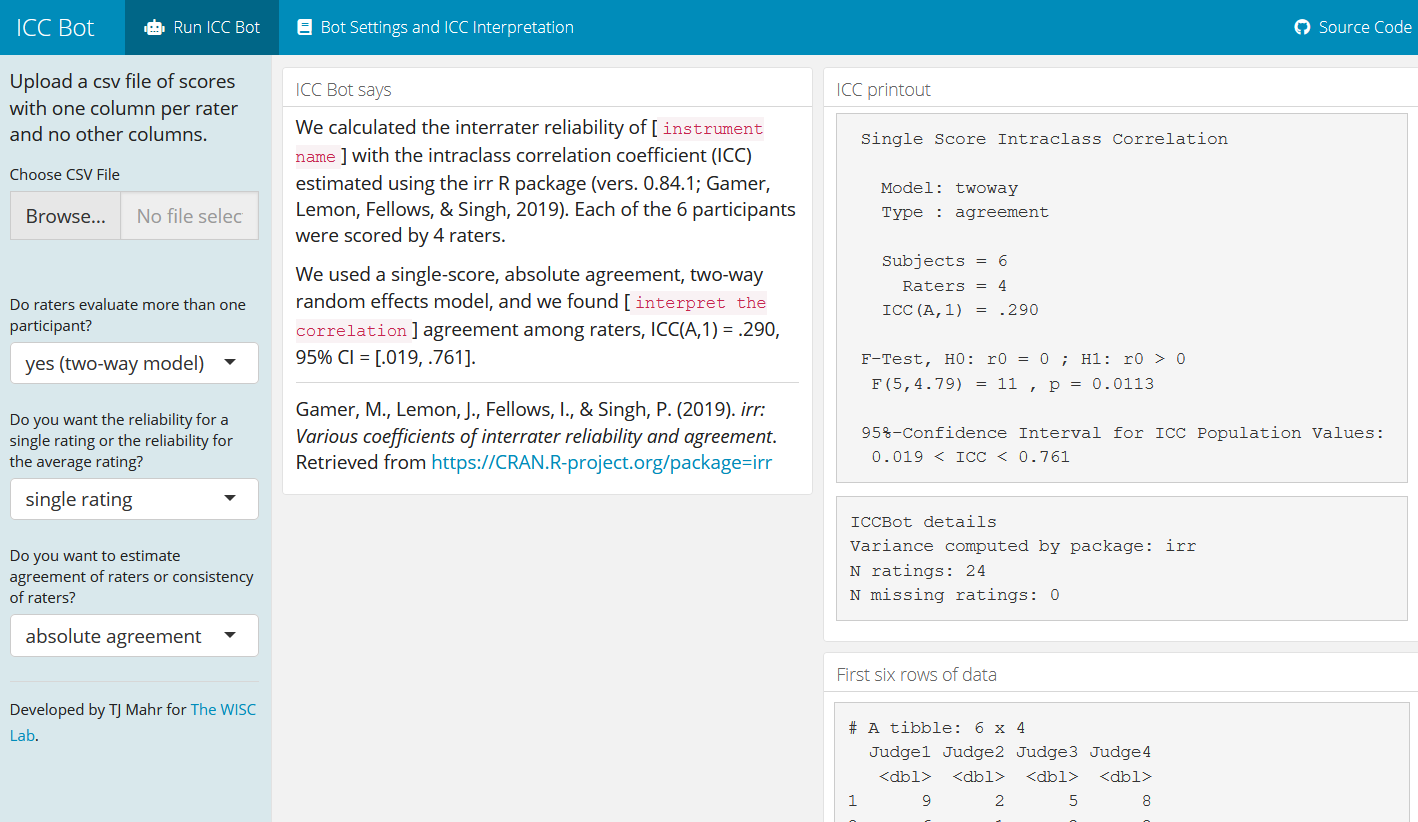
This statistic, as implemented in ICC Bot, only works at the summary score level (as opposed to the item score level). That is, the data should live in a table with one column per rater and one row per participant and with the cells being (total) scores. There should be one table cell per rater–participant pair.
There are a lot of ways to mix and match raters and participants, so there are many different flavors of ICC for specific rating situations. The ICC Bot supports six ICC types, so I try to provide detailed notes on the differences between these options on the Bot Settings and ICC Interpretation tab.
R Users. Because I have (only) 25 monthly hours of free compute time on ShinyApps.io, I ask that R users who want to try the app run it locally with:
# remotes::install_github("tjmahr/iccbot")
iccbot::run_app()
Everyone else. Because I have 25 monthly hours of free compute time on ShinyApps.io, you can try the app using https://tristan.shinyapps.io/iccbot/.
The rest of this post discusses the origin of the project and some programming details.
You can’t peek inside the scores (background)
“I feel like I’ve had an epiphany… It almost feels spiritual. All of the complexity in the data. It doesn’t matter.”
That was me, reporting to my group how we would handle interrater reliability for most of our tests. I had spent a few days in a rabbit-hole of interrater statistics: agreement percentages, Cohen’s kappa, other [last name]’s [Greek letter] statistics, “measurement equals true score plus error”, idemnotic versus vaganotic measurement, etc.
We give lots of speech and language tests in our lab, and we wanted to know how reliable our scores were for a particular test. The test is a fairly conventional articulation inventory. Children name pictures, and listeners score whether the child correctly produced certain target sounds. The words work through the consonants, consonant clusters, and vowels of English in different positions. For example, the sound /l/ is tested twice: in ladder (word-initially) and in ball (word-finally). The test weights some sounds are more than others. The vowel in knife is worth 3 points, the final /f/ .5 points. All told, there are 67 sounds tested and producing all of the sounds correctly yields an overall score of 100 points.
We had 2 graduate students each score 130 administrations of the test. We are talking about thousands of data points. The possible routes through the data are numerous To name a few options:
- Overall agreement percentage.
- Overall agreement percentage, weighting by item scores.
- Compute the agreement percentages by child, report the range.
- Weighted version of the above.
- Logistic mixed effects model with varying effects for child, item, and rater.
These statistics all answer interesting and important questions, especially for assessing rating fidelity or calibrating raters, but they are not the right questions. We are using the total scores from the test as a predictor of other measures. We want the reliability for those numbers. That was the epiphany. Report the reliability of the scores that are used in the analyses. It sounds basic and obvious, but my Bayesian training leads me to think about and model as much of the data-generating process as possible, so such a simplifying assumption felt like a revelation.
Because our field almost always uses summary score level measurements—that is, one single score on a test per participant—as speech and language measures, the ICC provides a general purpose statistic for computing interrater reliability. So I wrote an RMarkdown script to automatically populate a boilerplate paragraph with ICC statistics. Eventually, we came to report at least one ICC statistic in each of our papers, so we decided that this task should more automated and I turned my R script into a Shiny app.
How much work could it take? (technical details)
Like a lot of programming projects, the app started out simple: just a single file—a flexdashboard document, to be precise. And it grew organically, and by organically, I mean each change was easy and made sense but parts of it will look a little messy.
Initially, the app just translated the user input into arguments for
irr::icc(). Seriously, the code below shows the original code. input is
where user-input is stored in Shiny app, req() checks that inputs exist, so I
literally am translating form options into arguments for a function.
run_icc <- function() {
req(input$use_twoway_model)
req(input$single_or_average)
req(input$agreement_or_consistency)
model <- ifelse(
input$use_twoway_model == "yes (two-way model)",
"twoway",
"oneway"
)
unit <- ifelse(
input$single_or_average == "single rating",
"single",
"average"
)
type <- ifelse(
input$agreement_or_consistency == "absolute agreement",
"agreement",
"consistency"
)
add_formatted_results_to_icc(
irr::icc(
getData(),
model = model,
unit = unit,
type = type
)
)
}
Almost all of the work on the app was spent researching and writing the documentation to help users figure which inputs to use. I wrote an extensive section on how to choose the app settings and how to interpret ICC scores, and I checked my app’s results against the numbers in Shrout and Fleiss (1979), a landmark survey on ICC scores.
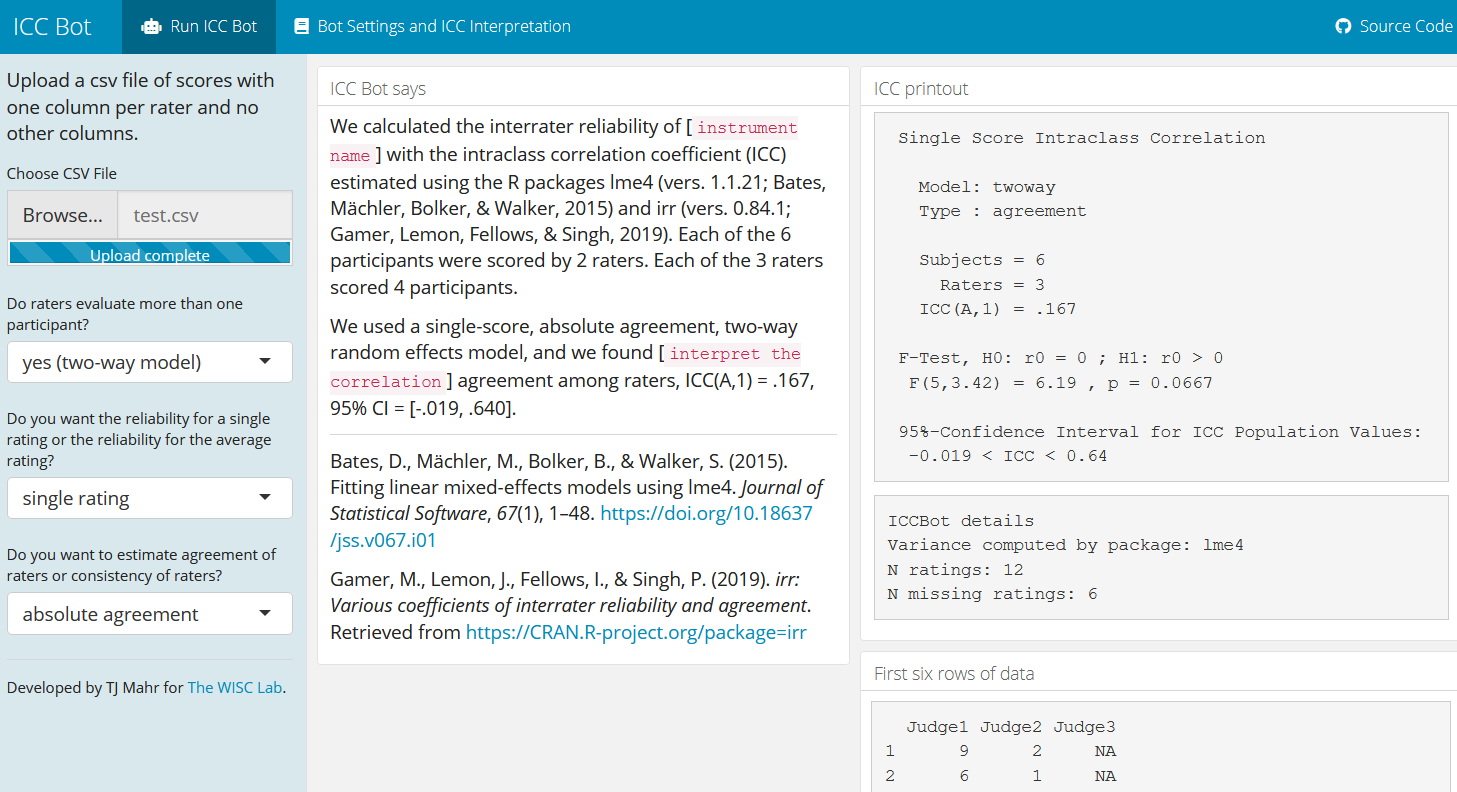
But I also had a worry. In the past, I’ve come across situations where raters and participants are not fully crossed. A typical situation is that there are a handful of available raters, so they work through the data until all the participants have two ratings. There is not a score for every combination of rater–participant; there is missing data.
Consider the following with 2 ratings per participant but 3 judges.
d <- iccbot::example_shrout_fleiss()
d[1:2, 3] <- NA
d[1:2 + 2, 2] <- NA
d[1:2 + 4, 1] <- NA
d <- d[-4]
d
#> # A tibble: 6 × 3
#> Judge1 Judge2 Judge3
#> <dbl> <dbl> <dbl>
#> 1 9 2 NA
#> 2 6 1 NA
#> 3 8 NA 6
#> 4 7 NA 2
#> 5 NA 5 6
#> 6 NA 2 4
irr::icc() handles this situation by removing any rows with missing data,
so it deletes everything. Look at those NAs.
irr::icc(d)
#> Warning in qf(1 - alpha/2, ns - 1, ns * (nr - 1)): NaNs produced
#> Warning in qf(1 - alpha/2, ns * (nr - 1), ns - 1): NaNs produced
#> Single Score Intraclass Correlation
#>
#> Model: oneway
#> Type : consistency
#>
#> Subjects = 0
#> Raters = 3
#> ICC(1) = NA
#>
#> F-Test, H0: r0 = 0 ; H1: r0 > 0
#> F(-1,0) = NA , p = NA
#>
#> 95%-Confidence Interval for ICC Population Values:
#> NA < ICC < NA
But we can compute an ICC on this data. If we fit a mixed model with by-participant and by-rater random effects, we get an estimate of the variances of the by-participant and by-rater and residual effects.
library(tidyverse)
# Convert to long format
d_long <- d %>%
tibble::rowid_to_column("participant") %>%
tidyr::gather(rater, score, -participant)
m <- lme4::lmer(
score ~ 1 + (1 | rater) + (1 | participant),
d_long
)
m
#> Linear mixed model fit by REML ['lmerMod']
#> Formula: score ~ 1 + (1 | rater) + (1 | participant)
#> Data: d_long
#> REML criterion at convergence: 47.4455
#> Random effects:
#> Groups Name Std.Dev.
#> participant (Intercept) 1.3027
#> rater (Intercept) 2.7301
#> Residual 0.9906
#> Number of obs: 12, groups: participant, 6; rater, 3
#> Fixed Effects:
#> (Intercept)
#> 4.833
See the Std.Dev. column? Compare the magnitude of the Residual row (1.0) to
the participant row (1.3) or the rater (2.7) row. Not much of the variance
is coming from the participant level.1 We can compute the ICC
as the proportion of the variance explained by the participant level directly
from these numbers.
variance_total <- sum(c(1.3, 2.7, 1.0) ^ 2)
variance_participant <- 1.3 ^ 2
variance_rater <- 2.7 ^ 2
variance_participant / variance_total
#> [1] 0.1693387
Indeed, this is what the implementation inside psych::ICC() does. It uses lme4
when it encounters missing data, so it gets the same answer. (Differences here
are due to rounding.)
psych::ICC(d)[["results"]]["Single_random_raters", ]
#> type ICC F df1 df2 p lower bound
#> Single_random_raters ICC2 0.1674984 6.188005 5 10 0.00725461 -0.01885906
#> upper bound
#> Single_random_raters 0.6404289
And this is what ICC Bot does too. If there is no missing data, irr::icc() runs
as normal. If there is missing data, the variance is computed with lme4 and then
the calculations in irr::icc() take place. I use the same code as irr::icc()
so that the results get printed just like the results from irr::icc().
iccbot::run_icc(d, model = "twoway", type = "agreement")
#> Single Score Intraclass Correlation
#>
#> Model: twoway
#> Type : agreement
#>
#> Subjects = 6
#> Raters = 3
#> ICC(A,1) = 0.167
#>
#> F-Test, H0: r0 = 0 ; H1: r0 > 0
#> F(5,3.42) = 6.19 , p = 0.0667
#>
#> 95%-Confidence Interval for ICC Population Values:
#> -0.019 < ICC < 0.64
Because the software that calculated changed behind the scenes, the citations inside the app change so that lme4 can properly credited.
If you do interrater reliability measures, let me know what works, what doesn’t work, what’s wrong and what’s confusing on the GitHub repository. Your feedback will help the app continue its organic growth.
Last knitted on 2022-05-27. Source code on GitHub.2
-
When they briefly cover the ICC, Gelman and Hill (2007) do something very cools with the numbers from the lme4 printout. They interpret the variances in terms of partial pooling. They are describing the example of repeated radon measurements in counties. They have σα (county) = .33 and σy (residual) = .76, so an ICC of .16.
One way to interpret the variation between counties, σα, is to consider the variance ratio, σα2/σy2, which inthis example is estimated at 0.332/0.762 = 0.19 or about one-fifth. Thus, the standard deviation of the average radon levels between counties is the same as the standard deviation of the average of 5 measurements within a county. […]
[…] The amount of information in this distribution is the same as that in 5 measurements within a county. To put it another way, for a country with a sample size of less than 5, there is more information in the group-level model than in the county’s data; for a county, with more than 5 observations, the within-country measurements are more informative (in the sense of providing a lower-variance estimate of the county’s average radon level.) As a result, the multilevel regression line in a county is closer to the complete-pooling estimate when sample size is less than 5 and, closer to the no-pooling estimate when the sample size exceeds 5.
-
.session_info #> ─ Session info ─────────────────────────────────────────────────────────────── #> setting value #> version R version 4.2.0 (2022-04-22 ucrt) #> os Windows 10 x64 (build 22000) #> system x86_64, mingw32 #> ui RTerm #> language (EN) #> collate English_United States.utf8 #> ctype English_United States.utf8 #> tz America/Chicago #> date 2022-05-27 #> pandoc NA #> #> ─ Packages ─────────────────────────────────────────────────────────────────── #> package * version date (UTC) lib source #> assertthat 0.2.1 2019-03-21 [1] CRAN (R 4.2.0) #> backports 1.4.1 2021-12-13 [1] CRAN (R 4.2.0) #> boot 1.3-28 2021-05-03 [2] CRAN (R 4.2.0) #> broom 0.8.0 2022-04-13 [1] CRAN (R 4.2.0) #> cellranger 1.1.0 2016-07-27 [1] CRAN (R 4.2.0) #> cli 3.3.0 2022-04-25 [1] CRAN (R 4.2.0) #> colorspace 2.0-3 2022-02-21 [1] CRAN (R 4.2.0) #> crayon 1.5.1 2022-03-26 [1] CRAN (R 4.2.0) #> DBI 1.1.2 2021-12-20 [1] CRAN (R 4.2.0) #> dbplyr 2.1.1 2021-04-06 [1] CRAN (R 4.2.0) #> dplyr * 1.0.9 2022-04-28 [1] CRAN (R 4.2.0) #> ellipsis 0.3.2 2021-04-29 [1] CRAN (R 4.2.0) #> evaluate 0.15 2022-02-18 [1] CRAN (R 4.2.0) #> fansi 1.0.3 2022-03-24 [1] CRAN (R 4.2.0) #> forcats * 0.5.1 2021-01-27 [1] CRAN (R 4.2.0) #> fs 1.5.2 2021-12-08 [1] CRAN (R 4.2.0) #> generics 0.1.2 2022-01-31 [1] CRAN (R 4.2.0) #> ggplot2 * 3.3.6 2022-05-03 [1] CRAN (R 4.2.0) #> git2r 0.30.1 2022-03-16 [1] CRAN (R 4.2.0) #> glue 1.6.2 2022-02-24 [1] CRAN (R 4.2.0) #> gtable 0.3.0 2019-03-25 [1] CRAN (R 4.2.0) #> haven 2.5.0 2022-04-15 [1] CRAN (R 4.2.0) #> here 1.0.1 2020-12-13 [1] CRAN (R 4.2.0) #> hms 1.1.1 2021-09-26 [1] CRAN (R 4.2.0) #> httr 1.4.3 2022-05-04 [1] CRAN (R 4.2.0) #> iccbot 0.0.2 2022-05-25 [1] Github (tjmahr/iccbot@b6c566d) #> irr 0.84.1 2019-01-26 [1] CRAN (R 4.2.0) #> jsonlite 1.8.0 2022-02-22 [1] CRAN (R 4.2.0) #> knitr * 1.39 2022-04-26 [1] CRAN (R 4.2.0) #> lattice 0.20-45 2021-09-22 [2] CRAN (R 4.2.0) #> lifecycle 1.0.1 2021-09-24 [1] CRAN (R 4.2.0) #> lme4 1.1-29 2022-04-07 [1] CRAN (R 4.2.0) #> lpSolve 5.6.15 2020-01-24 [1] CRAN (R 4.2.0) #> lubridate 1.8.0 2021-10-07 [1] CRAN (R 4.2.0) #> magrittr 2.0.3 2022-03-30 [1] CRAN (R 4.2.0) #> MASS 7.3-56 2022-03-23 [2] CRAN (R 4.2.0) #> Matrix 1.4-1 2022-03-23 [2] CRAN (R 4.2.0) #> minqa 1.2.4 2014-10-09 [1] CRAN (R 4.2.0) #> mnormt 2.0.2 2020-09-01 [1] CRAN (R 4.2.0) #> modelr 0.1.8 2020-05-19 [1] CRAN (R 4.2.0) #> munsell 0.5.0 2018-06-12 [1] CRAN (R 4.2.0) #> nlme 3.1-157 2022-03-25 [2] CRAN (R 4.2.0) #> nloptr 2.0.2 2022-05-19 [1] CRAN (R 4.2.0) #> pillar 1.7.0 2022-02-01 [1] CRAN (R 4.2.0) #> pkgconfig 2.0.3 2019-09-22 [1] CRAN (R 4.2.0) #> psych 2.2.5 2022-05-10 [1] CRAN (R 4.2.0) #> purrr * 0.3.4 2020-04-17 [1] CRAN (R 4.2.0) #> R6 2.5.1 2021-08-19 [1] CRAN (R 4.2.0) #> ragg 1.2.2 2022-02-21 [1] CRAN (R 4.2.0) #> Rcpp 1.0.8.3 2022-03-17 [1] CRAN (R 4.2.0) #> readr * 2.1.2 2022-01-30 [1] CRAN (R 4.2.0) #> readxl 1.4.0 2022-03-28 [1] CRAN (R 4.2.0) #> reprex 2.0.1 2021-08-05 [1] CRAN (R 4.2.0) #> rlang 1.0.2 2022-03-04 [1] CRAN (R 4.2.0) #> rprojroot 2.0.3 2022-04-02 [1] CRAN (R 4.2.0) #> rstudioapi 0.13 2020-11-12 [1] CRAN (R 4.2.0) #> rvest 1.0.2 2021-10-16 [1] CRAN (R 4.2.0) #> scales 1.2.0 2022-04-13 [1] CRAN (R 4.2.0) #> sessioninfo 1.2.2 2021-12-06 [1] CRAN (R 4.2.0) #> stringi 1.7.6 2021-11-29 [1] CRAN (R 4.2.0) #> stringr * 1.4.0 2019-02-10 [1] CRAN (R 4.2.0) #> systemfonts 1.0.4 2022-02-11 [1] CRAN (R 4.2.0) #> textshaping 0.3.6 2021-10-13 [1] CRAN (R 4.2.0) #> tibble * 3.1.7 2022-05-03 [1] CRAN (R 4.2.0) #> tidyr * 1.2.0 2022-02-01 [1] CRAN (R 4.2.0) #> tidyselect 1.1.2 2022-02-21 [1] CRAN (R 4.2.0) #> tidyverse * 1.3.1 2021-04-15 [1] CRAN (R 4.2.0) #> tmvnsim 1.0-2 2016-12-15 [1] CRAN (R 4.2.0) #> tzdb 0.3.0 2022-03-28 [1] CRAN (R 4.2.0) #> utf8 1.2.2 2021-07-24 [1] CRAN (R 4.2.0) #> vctrs 0.4.1 2022-04-13 [1] CRAN (R 4.2.0) #> withr 2.5.0 2022-03-03 [1] CRAN (R 4.2.0) #> xfun 0.31 2022-05-10 [1] CRAN (R 4.2.0) #> xml2 1.3.3 2021-11-30 [1] CRAN (R 4.2.0) #> #> [1] C:/Users/Tristan/AppData/Local/R/win-library/4.2 #> [2] C:/Program Files/R/R-4.2.0/library #> #> ──────────────────────────────────────────────────────────────────────────────

Leave a comment