New package polypoly (helper functions for orthogonal polynomials)
Last week, I released a new package called polypoly to CRAN. It wraps up some common tasks for dealing with orthogonal polynomials into a single package. The README shows off the main functionality, as well as the neat “logo” I made for the package. In this post, I use the package on some word recognition data.
Demo: Growth curve analysis
I primarily use orthogonal polynomials to model data from eyetracking experiments where growth curves describe how the probability of looking at a image changes as the image is named. The analysis technique, including orthogonal polynomials and mixed effects models of eyetracking data, are described in Mirman’s 2014 book.
In our 2015 paper, toddlers saw two images on a computer screen. The objects in the images started with different consonants: for example, duck and ball. The toddlers heard sentences like “find the ball”, and we measured how their gaze location onscreen changed in response to speech. This setup is a pretty standard procedure for studying spoken word recognition.
We manipulated the vowel in the word the. In the facilitating condition, the vowel has acoustic information (via anticipatory coarticulation) which would allow an adult listener to predict the upcoming consonant. In the neutral condition, the vowel provides no cues about the upcoming consonant. The scientific question is whether these kiddos can take advantage of these acoustic cues during word recognition.
Here’s how the data look, both in R and in a plot.
library(ggplot2)
library(dplyr)
# The data
d
#> # A tibble: 986 × 6
#> Subj Condition Time ToDistractor ToTarget Proportion
#> <int> <chr> <int> <int> <int> <dbl>
#> 1 1 facilitating 200 9 9 0.5
#> 2 1 facilitating 250 9 10 0.526
#> 3 1 facilitating 300 6 12 0.667
#> 4 1 facilitating 350 6 12 0.667
#> 5 1 facilitating 400 6 12 0.667
#> 6 1 facilitating 450 6 12 0.667
#> 7 1 facilitating 500 6 12 0.667
#> 8 1 facilitating 550 6 12 0.667
#> 9 1 facilitating 600 4 12 0.75
#> 10 1 facilitating 650 3 15 0.833
#> # … with 976 more rows
# Helper dataframe of where to put condition labels on the next plot
df_labs <- tibble(
Time = c(650, 800),
Proportion = c(.775, .625),
Condition = c("facilitating", "neutral")
)
p <- ggplot(d) +
aes(x = Time, y = Proportion, color = Condition) +
geom_hline(yintercept = .5, size = 2, color = "white") +
stat_summary(fun.data = mean_se) +
geom_text(aes(label = Condition), data = df_labs, size = 6) +
labs(
x = "Time after noun onset [ms]",
y = "Proportion looks to named image",
caption = "Mean ± SE. N = 29 children."
) +
guides(color = "none")
p
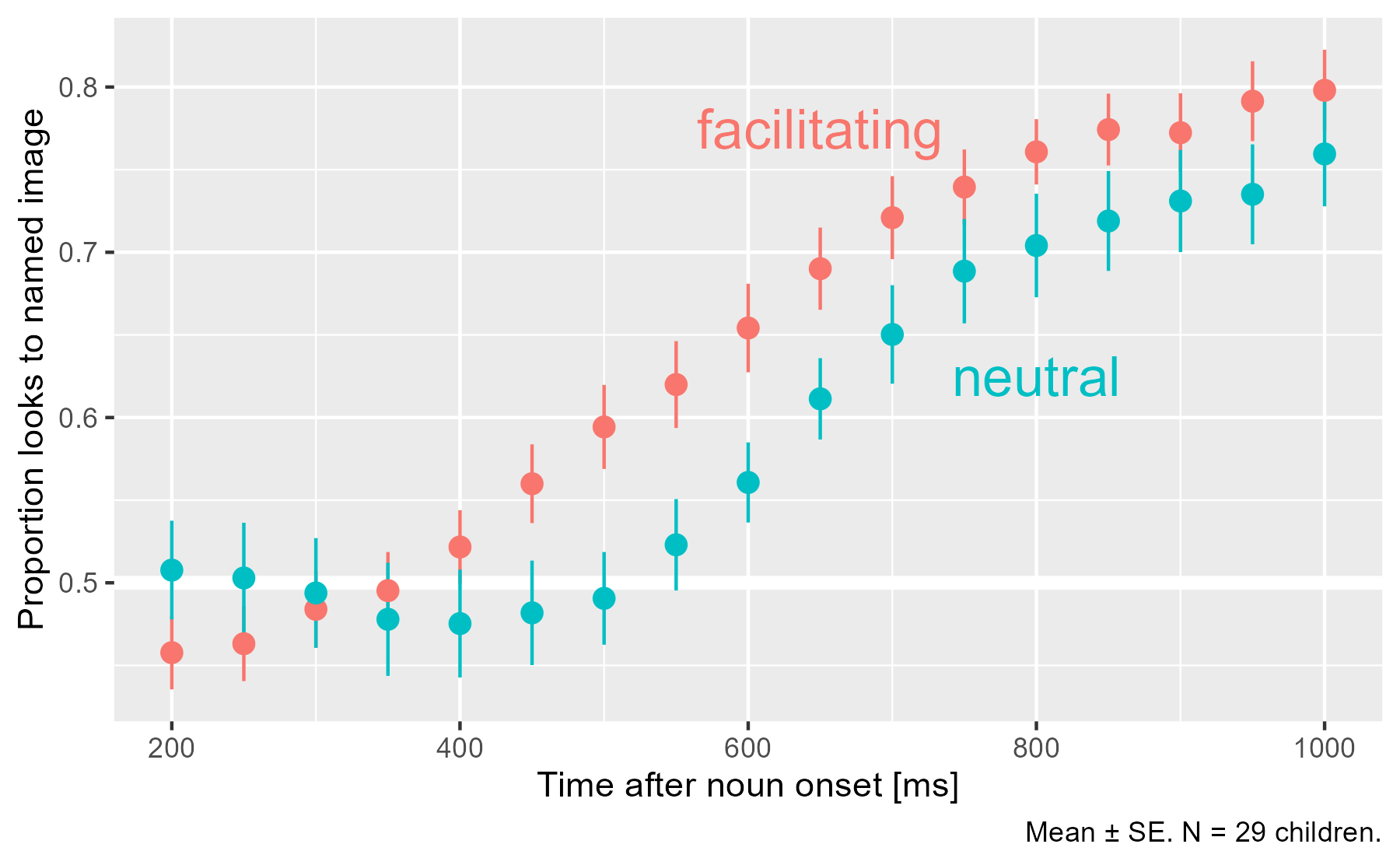
Early on, children look equal amounts to both images on average (.5), and the proportion of looks to the named image increase as the word unfolds. In the facilitating condition, that rise happens earlier.
We fit a mixed-effects logistic regression model to estimate how the probability of looking to the named image changes over time, across conditions, and within children. We use cubic orthogonal polynomials to represent Time. For each time point, we have three predictors available to us: Time1, Time2, and Time3. (Plus, there’s a constant “intercept” term.) Our model’s growth curve will be a weighted combination of these polynomial curves. The code below shows off about half the functionality of the package :bowtie::
poly(unique(d$Time), 3) %>%
# Force Time^1 term to range from -.5 to .5. Rescale others accordingly.
polypoly::poly_rescale(scale_width = 1) %>%
polypoly::poly_plot()
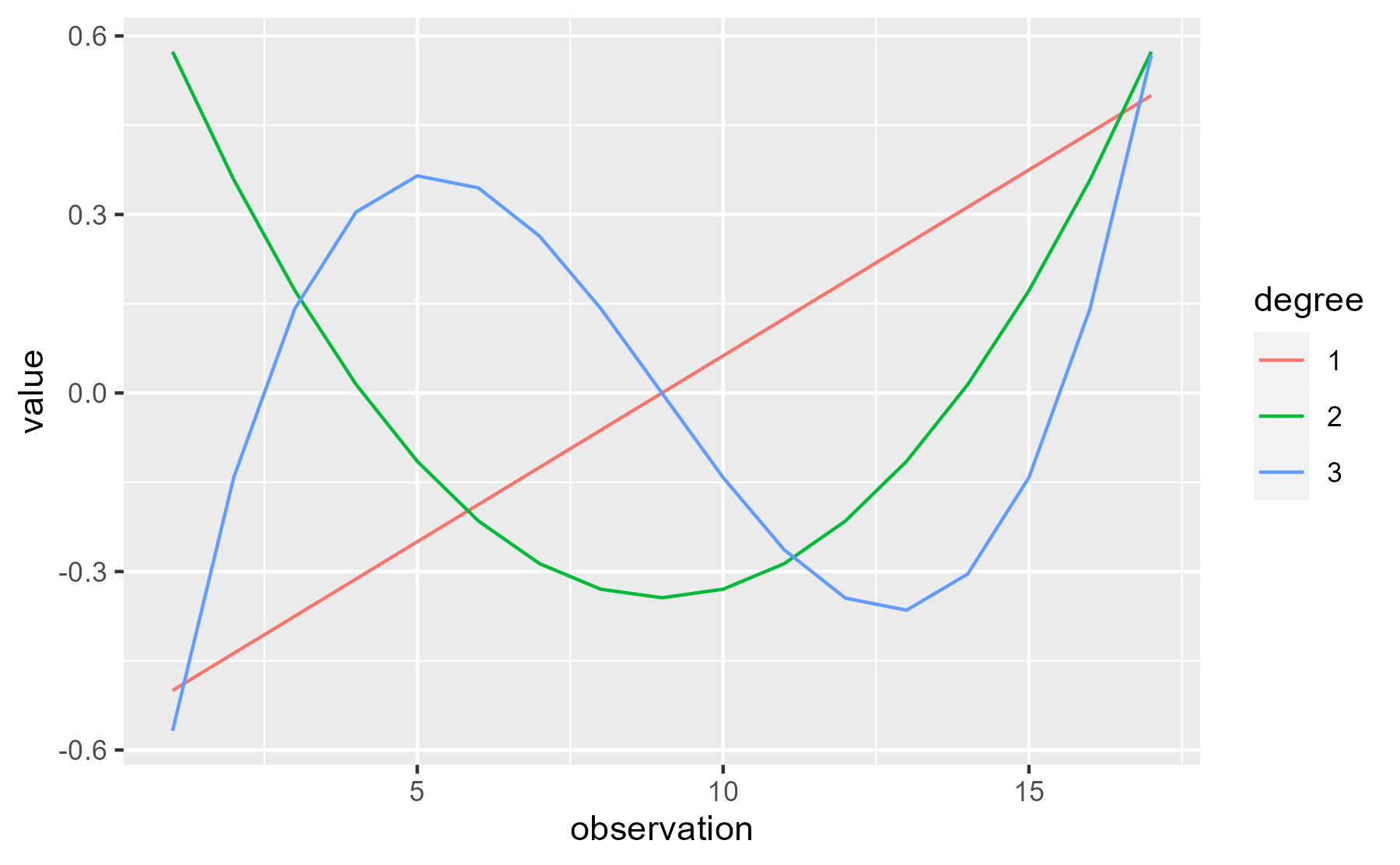
I think people sometimes describe the contributions of these curves to the overall growth curve as trends: “A negative linear trend”, “a significant quadratic trend”, etc. I like that word because it makes the terminology a little less intimidating.
Quick aside: Why orthogonal polynomials?
Why do we use orthogonal polynomial terms? First, note that simple polynomials x, x2 and x3 are correlated. Orthogonal ones are not correlated. (Hence, the name.)
# Simple
poly(1:10, 3, raw = TRUE) %>%
cor() %>%
round(2)
#> 1 2 3
#> 1 1.00 0.97 0.93
#> 2 0.97 1.00 0.99
#> 3 0.93 0.99 1.00
# Orthogonal
poly(1:10, 3, raw = FALSE) %>%
cor() %>%
round(2)
#> 1 2 3
#> 1 1 0 0
#> 2 0 1 0
#> 3 0 0 1
Adding new correlated predictors to a model is a problem. The parameter estimates will change as different predictors are added. Here we simulate some fake data, and fit three models with 1-, 2- and 3-degree raw polynomials.
# for reproducible blogging
set.seed(20210215)
x <- 1:10
y <- x +
rnorm(1, mean = 100) * (x) +
rnorm(1, mean = 0, sd = .01) * (x) ^ 2 +
rnorm(1, mean = -1) * (x) ^ 3 +
rnorm(10)
models <- list(
m1 = lm(y ~ x),
m2 = lm(y ~ x + I(x^2)),
m3 = lm(y ~ x + I(x^2) + I(x^3))
)
As expected, the estimates for the effects change from model to model:
models %>%
lapply(broom::tidy) %>%
bind_rows(.id = "model") %>%
select(model:estimate) %>%
mutate(estimate = round(estimate, 2))
#> # A tibble: 9 × 3
#> model term estimate
#> <chr> <chr> <dbl>
#> 1 m1 (Intercept) 626.
#> 2 m1 x -136.
#> 3 m2 (Intercept) -194.
#> 4 m2 x 275.
#> 5 m2 I(x^2) -37.3
#> 6 m3 (Intercept) -0.43
#> 7 m3 x 103.
#> 8 m3 I(x^2) -0.08
#> 9 m3 I(x^3) -2.25
But with orthogonal polynomials, the parameter estimates don’t change from model to model.
models2 <- list(
m1 = lm(y ~ poly(x, 1)),
m2 = lm(y ~ poly(x, 2)),
m3 = lm(y ~ poly(x, 3))
)
models2 %>%
lapply(broom::tidy) %>%
bind_rows(.id = "model") %>%
select(model:estimate) %>%
mutate(estimate = round(estimate, 2))
#> # A tibble: 9 × 3
#> model term estimate
#> <chr> <chr> <dbl>
#> 1 m1 (Intercept) -119.
#> 2 m1 poly(x, 1) -1231.
#> 3 m2 (Intercept) -119.
#> 4 m2 poly(x, 2)1 -1231.
#> 5 m2 poly(x, 2)2 -857.
#> 6 m3 (Intercept) -119.
#> 7 m3 poly(x, 3)1 -1231.
#> 8 m3 poly(x, 3)2 -857.
#> 9 m3 poly(x, 3)3 -125.
That’s probably the simplest reason why orthogonal polynomials are preferred. (I can’t remember any others right now.)
Back to the data
Before fitting the model, I use poly_add_columns() to add polynomial terms as
columns to the dataframe. (For speed here, I use a simplified random effects
structure, estimating growth curve parameters for each Child x Condition
combination.)
library(lme4)
d <- d %>%
polypoly::poly_add_columns(
Time,
degree = 3,
prefix = "ot",
scale_width = 1
) %>%
# Change the reference level
mutate(Condition = factor(Condition, c("neutral", "facilitating")))
m <- glmer(
cbind(ToTarget, ToDistractor) ~
(ot1 + ot2 + ot3) * Condition +
(ot1 + ot2 + ot3 | Subj:Condition),
family = binomial,
data = d)
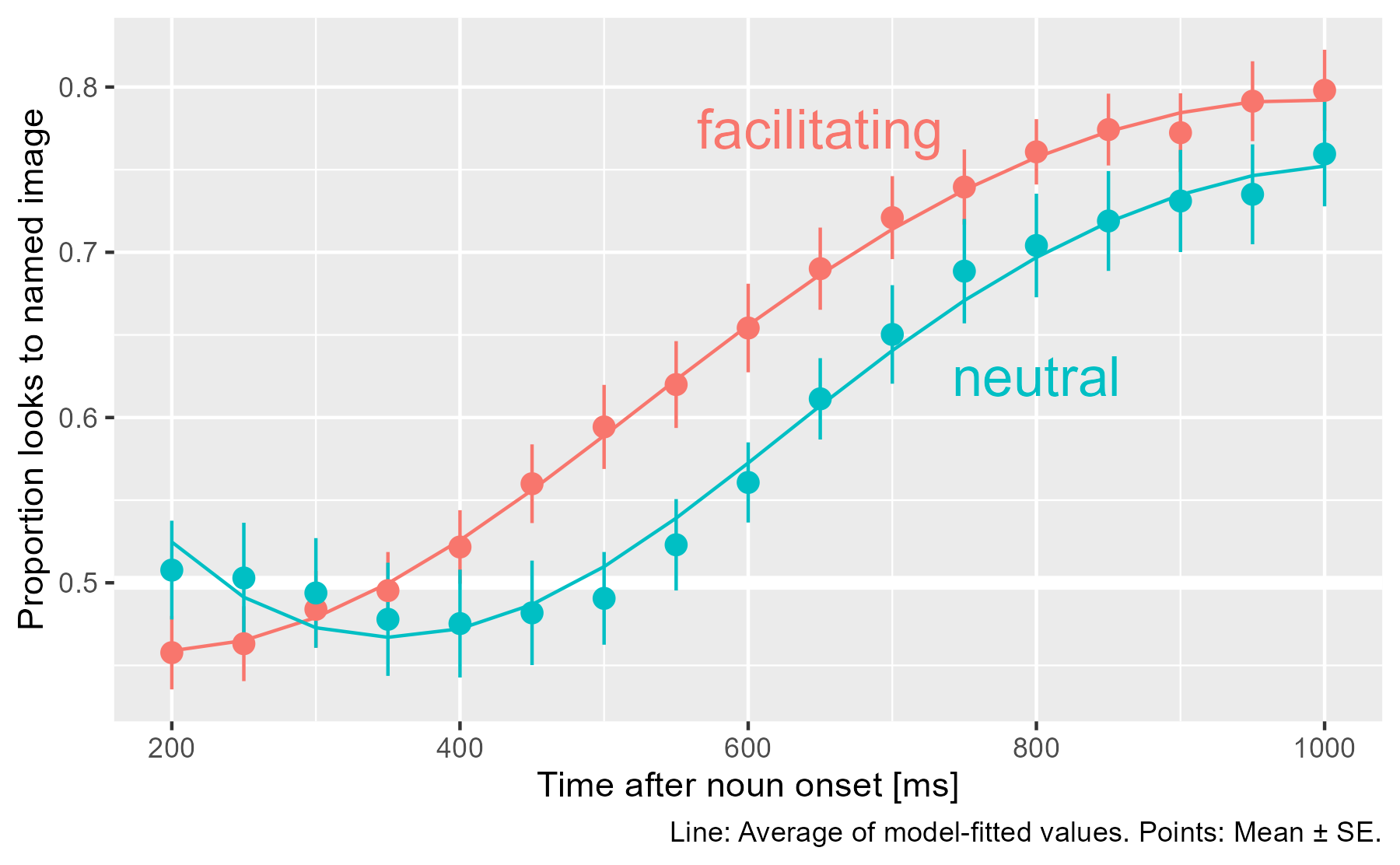
We can confirm that the model captures the overall shape of the growth curves.
# The lines here are not quite the overall average, but the averages of 29
# individual fits (for each participant). That's why the caption is a little
# weird.
p +
stat_summary(aes(y = fitted(m)), fun = mean, geom = "line") +
labs(caption = "Line: Average of model-fitted values. Points: Mean ± SE.")
We can inspect the model summary as well.
arm::display(m)
#> glmer(formula = cbind(ToTarget, ToDistractor) ~ (ot1 + ot2 +
#> ot3) * Condition + (ot1 + ot2 + ot3 | Subj:Condition), data = d,
#> family = binomial)
#> coef.est coef.se
#> (Intercept) 0.47 0.10
#> ot1 1.57 0.28
#> ot2 0.45 0.11
#> ot3 -0.34 0.09
#> Conditionfacilitating 0.23 0.14
#> ot1:Conditionfacilitating 0.45 0.39
#> ot2:Conditionfacilitating -0.44 0.16
#> ot3:Conditionfacilitating 0.11 0.13
#>
#> Error terms:
#> Groups Name Std.Dev. Corr
#> Subj:Condition (Intercept) 0.53
#> ot1 1.46 0.23
#> ot2 0.52 -0.05 0.31
#> ot3 0.39 -0.08 -0.64 0.09
#> Residual 1.00
#> ---
#> number of obs: 986, groups: Subj:Condition, 58
#> AIC = 4788.2, DIC = -3961.1
#> deviance = 395.6
The model summary indicates a significant Condition x Time2 interaction, but really, only the intercept and Time1 can ever be interpreted directly. To understand the model fit, we visualize how each of the polynomial terms are weighted.
Here we create a matrix of the polynomial terms plus a column of ones for the intercept.
time_mat <- poly(sort(unique(d$Time)), 3) %>%
polypoly::poly_rescale(1) %>%
cbind(constant = 1, .)
round(time_mat, 2)
#> constant 1 2 3
#> [1,] 1 -0.50 0.57 -0.57
#> [2,] 1 -0.44 0.36 -0.14
#> [3,] 1 -0.37 0.17 0.14
#> [4,] 1 -0.31 0.01 0.30
#> [5,] 1 -0.25 -0.11 0.36
#> [6,] 1 -0.19 -0.22 0.34
#> [7,] 1 -0.12 -0.29 0.26
#> [8,] 1 -0.06 -0.33 0.14
#> [9,] 1 0.00 -0.34 0.00
#> [10,] 1 0.06 -0.33 -0.14
#> [11,] 1 0.12 -0.29 -0.26
#> [12,] 1 0.19 -0.22 -0.34
#> [13,] 1 0.25 -0.11 -0.36
#> [14,] 1 0.31 0.01 -0.30
#> [15,] 1 0.37 0.17 -0.14
#> [16,] 1 0.44 0.36 0.14
#> [17,] 1 0.50 0.57 0.57
To compute the weighted values, we multiply by a diagonal matrix of the coefficients.
neut_coefs <- fixef(m)[1:4]
faci_coefs <- neut_coefs + fixef(m)[5:8]
faci_coefs
#> (Intercept) ot1 ot2 ot3
#> 0.699914630 2.014092454 0.006641487 -0.226682309
set_colnames <- `colnames<-`
m_neut <- time_mat %*% diag(neut_coefs) %>%
set_colnames(c("constant", "ot1", "ot2", "ot3"))
m_faci <- time_mat %*% diag(faci_coefs) %>%
set_colnames(c("constant", "ot1", "ot2", "ot3"))
# Convince ourselves with an example
round(m_faci, 2)
#> constant ot1 ot2 ot3
#> [1,] 0.7 -1.01 0 0.13
#> [2,] 0.7 -0.88 0 0.03
#> [3,] 0.7 -0.76 0 -0.03
#> [4,] 0.7 -0.63 0 -0.07
#> [5,] 0.7 -0.50 0 -0.08
#> [6,] 0.7 -0.38 0 -0.08
#> [7,] 0.7 -0.25 0 -0.06
#> [8,] 0.7 -0.13 0 -0.03
#> [9,] 0.7 0.00 0 0.00
#> [10,] 0.7 0.13 0 0.03
#> [11,] 0.7 0.25 0 0.06
#> [12,] 0.7 0.38 0 0.08
#> [13,] 0.7 0.50 0 0.08
#> [14,] 0.7 0.63 0 0.07
#> [15,] 0.7 0.76 0 0.03
#> [16,] 0.7 0.88 0 -0.03
#> [17,] 0.7 1.01 0 -0.13
Then, we can use the poly_melt() function to get a dataframe from each
weighted matrix and then plot each of the effects.
df_neut <- m_neut %>%
polypoly::poly_melt() %>%
tibble::add_column(Condition = "neutral")
df_faci <- m_faci %>%
polypoly::poly_melt() %>%
tibble::add_column(Condition = "facilitating")
df_both <- bind_rows(df_faci, df_neut) %>%
mutate(Condition = factor(Condition, c("neutral", "facilitating")))
ggplot(df_both) +
aes(x = observation, y = value, color = Condition) +
geom_line() +
facet_wrap("degree")
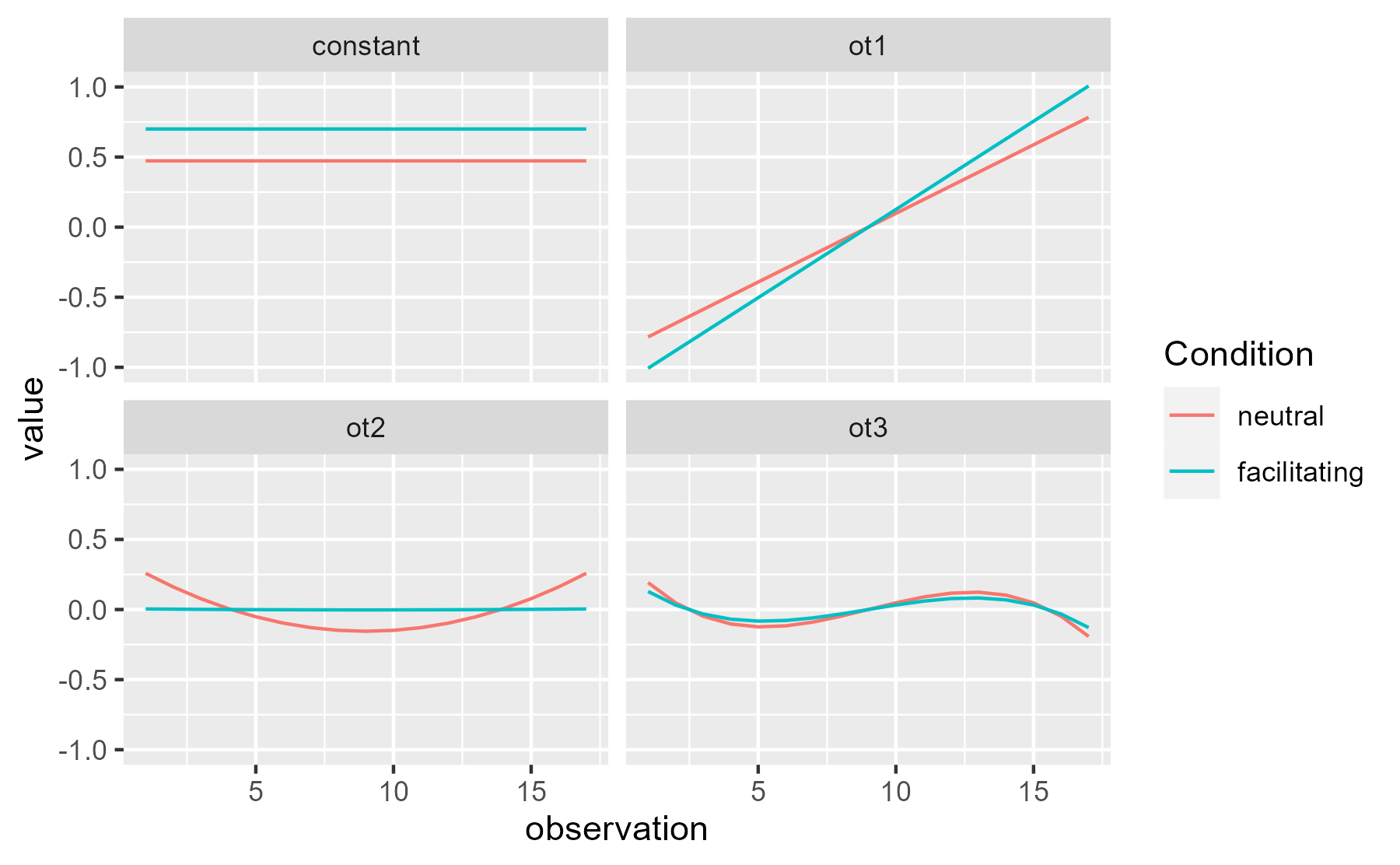
Visually, the quadratic effect on the neutral curve pulls down the values during the center (when the curves are most different) and pushes the values in the tails upwards (when the curves are closest). Although only the quadratic effect is nominally significant, the constant and linear terms suggest other smaller effects but they are too noisy to pin down.
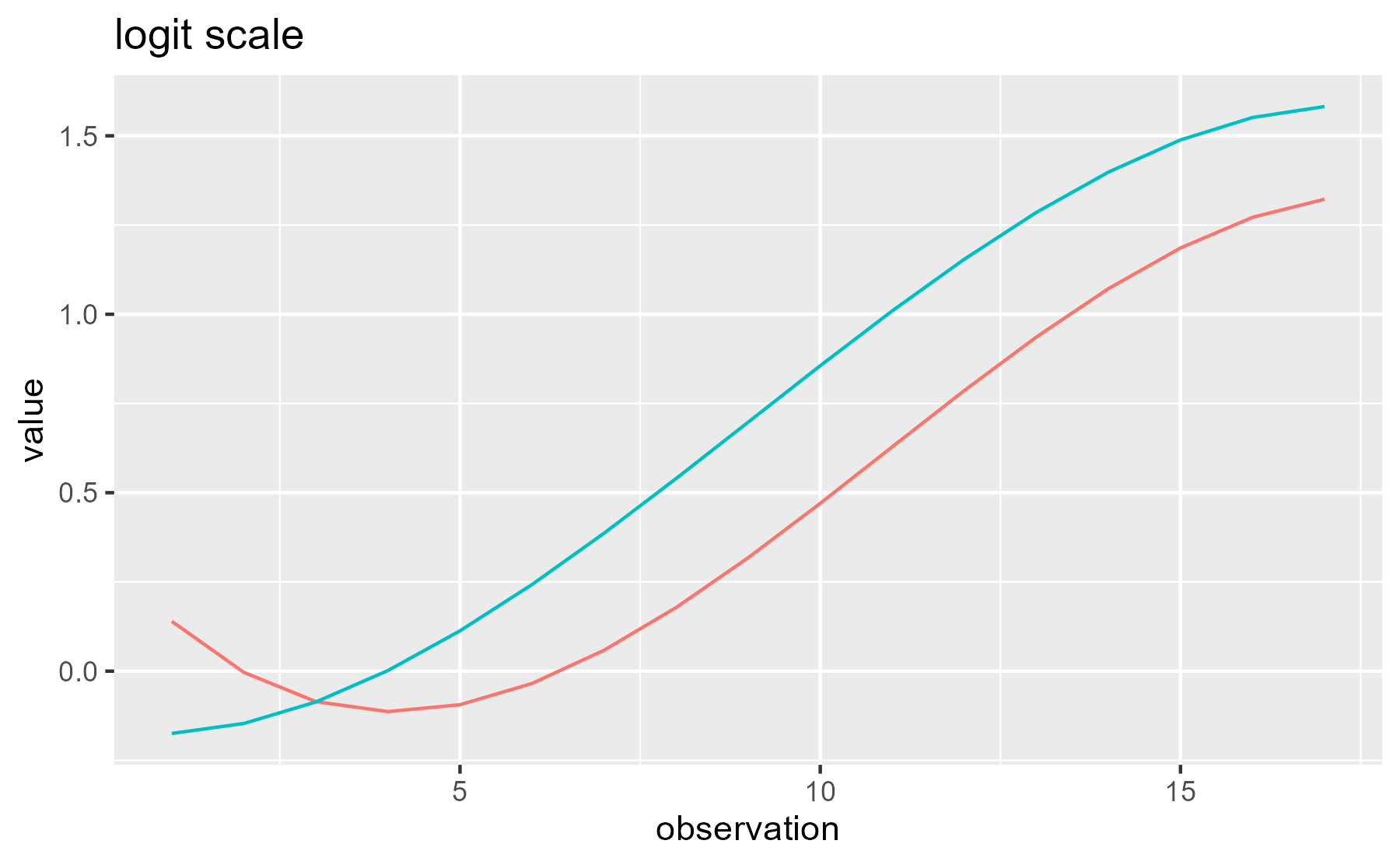
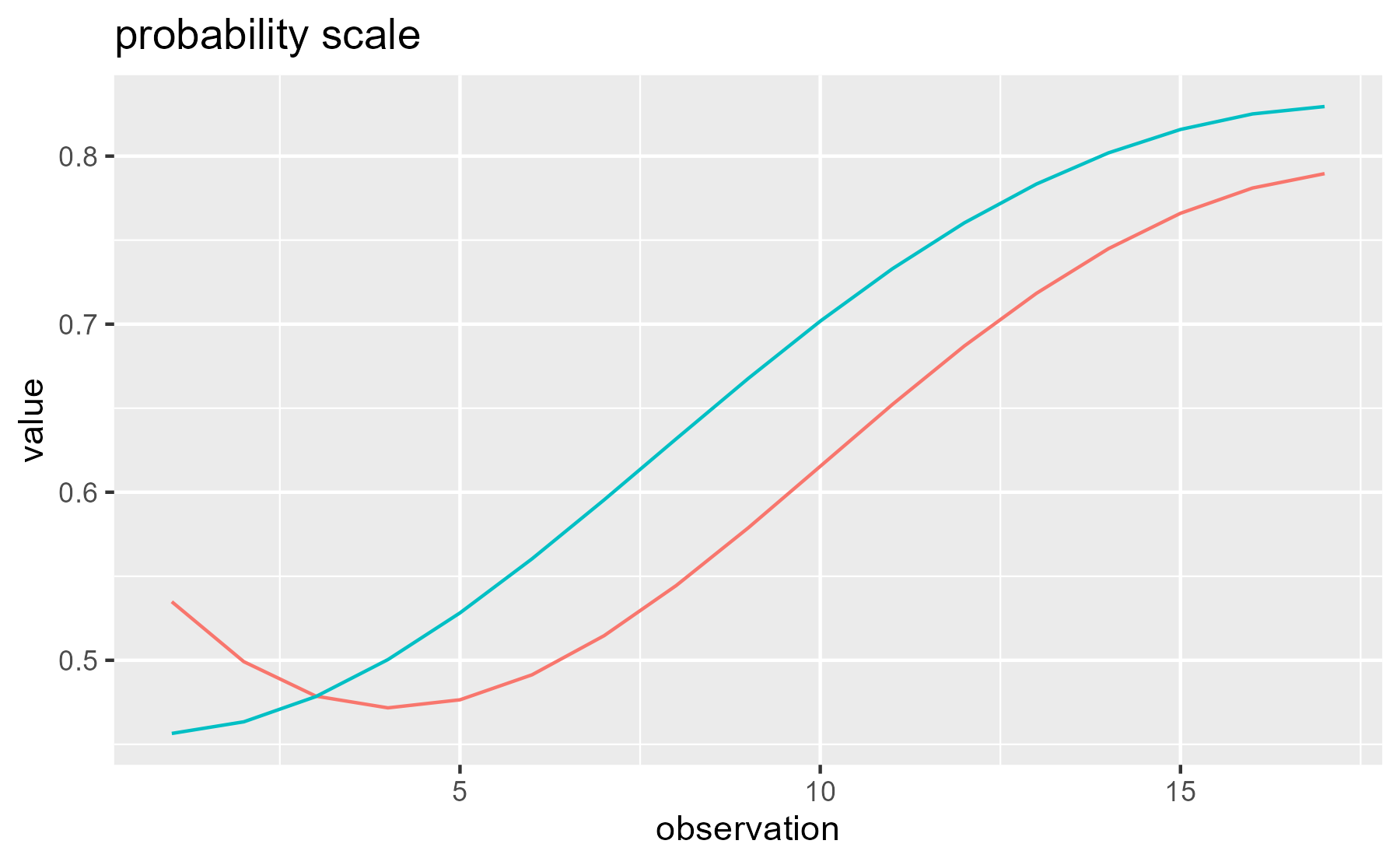
It’s worth noting that the predictors and weights discussed above are on the log-odds/logit scale used inside of the model, instead of the proportion scale used in the plots of the data and model fits. Basically, these weighted values are summed together and then squeezed into the range [0, 1] with a nonlinear transformation. For these data, the two scales produce similar looking growth curves, but you can notice that the right end of the curves are pinched slightly closer together in the probability-scale plot:
ggplot(df_both) +
aes(x = observation, y = value, color = Condition) +
stat_summary(fun = sum, geom = "line") +
ggtitle("logit scale") +
guides(color = "none")
ggplot(df_both) +
aes(x = observation, y = value, color = Condition) +
stat_summary(fun = function(xs) plogis(sum(xs)), geom = "line") +
ggtitle("probability scale") +
guides(color = "none")
Last knitted on 2022-05-27. Source code on GitHub.1
-
.session_info #> ─ Session info ─────────────────────────────────────────────────────────────── #> setting value #> version R version 4.2.0 (2022-04-22 ucrt) #> os Windows 10 x64 (build 22000) #> system x86_64, mingw32 #> ui RTerm #> language (EN) #> collate English_United States.utf8 #> ctype English_United States.utf8 #> tz America/Chicago #> date 2022-05-27 #> pandoc NA #> #> ─ Packages ─────────────────────────────────────────────────────────────────── #> package * version date (UTC) lib source #> abind 1.4-5 2016-07-21 [1] CRAN (R 4.2.0) #> arm 1.12-2 2021-10-15 [1] CRAN (R 4.2.0) #> assertthat 0.2.1 2019-03-21 [1] CRAN (R 4.2.0) #> backports 1.4.1 2021-12-13 [1] CRAN (R 4.2.0) #> bit 4.0.4 2020-08-04 [1] CRAN (R 4.2.0) #> bit64 4.0.5 2020-08-30 [1] CRAN (R 4.2.0) #> boot 1.3-28 2021-05-03 [2] CRAN (R 4.2.0) #> broom 0.8.0 2022-04-13 [1] CRAN (R 4.2.0) #> cli 3.3.0 2022-04-25 [1] CRAN (R 4.2.0) #> coda 0.19-4 2020-09-30 [1] CRAN (R 4.2.0) #> colorspace 2.0-3 2022-02-21 [1] CRAN (R 4.2.0) #> crayon 1.5.1 2022-03-26 [1] CRAN (R 4.2.0) #> curl 4.3.2 2021-06-23 [1] CRAN (R 4.2.0) #> DBI 1.1.2 2021-12-20 [1] CRAN (R 4.2.0) #> digest 0.6.29 2021-12-01 [1] CRAN (R 4.2.0) #> dplyr * 1.0.9 2022-04-28 [1] CRAN (R 4.2.0) #> ellipsis 0.3.2 2021-04-29 [1] CRAN (R 4.2.0) #> evaluate 0.15 2022-02-18 [1] CRAN (R 4.2.0) #> fansi 1.0.3 2022-03-24 [1] CRAN (R 4.2.0) #> farver 2.1.0 2021-02-28 [1] CRAN (R 4.2.0) #> generics 0.1.2 2022-01-31 [1] CRAN (R 4.2.0) #> ggplot2 * 3.3.6 2022-05-03 [1] CRAN (R 4.2.0) #> git2r 0.30.1 2022-03-16 [1] CRAN (R 4.2.0) #> glue 1.6.2 2022-02-24 [1] CRAN (R 4.2.0) #> gtable 0.3.0 2019-03-25 [1] CRAN (R 4.2.0) #> here 1.0.1 2020-12-13 [1] CRAN (R 4.2.0) #> highr 0.9 2021-04-16 [1] CRAN (R 4.2.0) #> hms 1.1.1 2021-09-26 [1] CRAN (R 4.2.0) #> knitr * 1.39 2022-04-26 [1] CRAN (R 4.2.0) #> labeling 0.4.2 2020-10-20 [1] CRAN (R 4.2.0) #> lattice 0.20-45 2021-09-22 [2] CRAN (R 4.2.0) #> lifecycle 1.0.1 2021-09-24 [1] CRAN (R 4.2.0) #> lme4 * 1.1-29 2022-04-07 [1] CRAN (R 4.2.0) #> magrittr 2.0.3 2022-03-30 [1] CRAN (R 4.2.0) #> MASS 7.3-56 2022-03-23 [2] CRAN (R 4.2.0) #> Matrix * 1.4-1 2022-03-23 [2] CRAN (R 4.2.0) #> minqa 1.2.4 2014-10-09 [1] CRAN (R 4.2.0) #> munsell 0.5.0 2018-06-12 [1] CRAN (R 4.2.0) #> nlme 3.1-157 2022-03-25 [2] CRAN (R 4.2.0) #> nloptr 2.0.2 2022-05-19 [1] CRAN (R 4.2.0) #> pillar 1.7.0 2022-02-01 [1] CRAN (R 4.2.0) #> pkgconfig 2.0.3 2019-09-22 [1] CRAN (R 4.2.0) #> plyr 1.8.7 2022-03-24 [1] CRAN (R 4.2.0) #> polypoly 0.0.2 2017-05-27 [1] CRAN (R 4.2.0) #> purrr 0.3.4 2020-04-17 [1] CRAN (R 4.2.0) #> R6 2.5.1 2021-08-19 [1] CRAN (R 4.2.0) #> ragg 1.2.2 2022-02-21 [1] CRAN (R 4.2.0) #> Rcpp 1.0.8.3 2022-03-17 [1] CRAN (R 4.2.0) #> readr * 2.1.2 2022-01-30 [1] CRAN (R 4.2.0) #> reshape2 1.4.4 2020-04-09 [1] CRAN (R 4.2.0) #> rlang 1.0.2 2022-03-04 [1] CRAN (R 4.2.0) #> rprojroot 2.0.3 2022-04-02 [1] CRAN (R 4.2.0) #> rstudioapi 0.13 2020-11-12 [1] CRAN (R 4.2.0) #> scales 1.2.0 2022-04-13 [1] CRAN (R 4.2.0) #> sessioninfo 1.2.2 2021-12-06 [1] CRAN (R 4.2.0) #> stringi 1.7.6 2021-11-29 [1] CRAN (R 4.2.0) #> stringr 1.4.0 2019-02-10 [1] CRAN (R 4.2.0) #> systemfonts 1.0.4 2022-02-11 [1] CRAN (R 4.2.0) #> textshaping 0.3.6 2021-10-13 [1] CRAN (R 4.2.0) #> tibble 3.1.7 2022-05-03 [1] CRAN (R 4.2.0) #> tidyr 1.2.0 2022-02-01 [1] CRAN (R 4.2.0) #> tidyselect 1.1.2 2022-02-21 [1] CRAN (R 4.2.0) #> tzdb 0.3.0 2022-03-28 [1] CRAN (R 4.2.0) #> utf8 1.2.2 2021-07-24 [1] CRAN (R 4.2.0) #> vctrs 0.4.1 2022-04-13 [1] CRAN (R 4.2.0) #> vroom 1.5.7 2021-11-30 [1] CRAN (R 4.2.0) #> withr 2.5.0 2022-03-03 [1] CRAN (R 4.2.0) #> xfun 0.31 2022-05-10 [1] CRAN (R 4.2.0) #> #> [1] C:/Users/Tristan/AppData/Local/R/win-library/4.2 #> [2] C:/Program Files/R/R-4.2.0/library #> #> ──────────────────────────────────────────────────────────────────────────────

Leave a comment