10 PRINT mazes with ggplot2
There is a celebrated Commodore 64 program that randomly prints outs /
and \ characters and fills the screen with neat-looking maze designs.
It is just one line of code, but there is
a whole book written about it.
10 PRINT CHR$(205.5+RND(1)); : GOTO 10

The basic idea, from my reading of the code, is that CHR$(205) is \,
CHR$(206) is /, and the program randomly selects between the two by
adding a random number to 205.5. Endlessly looping over this command
fills the screen with that pleasing maze pattern.
In R, we could replicate this functionality with by randomly sampling the slashes:
set.seed(20210215)
sample_n_slashes <- function(n) {
sample(c("/", "\\"), size = n, replace = TRUE)
}
withr::with_options(
list(width = 40),
cat(sample_n_slashes(800), sep = "", fill = TRUE)
)
#> ////\\///\//\\\/\\\\//\/////////\///////
#> /\\\////\\\\\//\\/\\\///\///\/////\///\/
#> /\\/\////////\/\\/\/////////\\\\//\\\\\/
#> \///\//\/\\/\//\\\\//\\///\\//\\\\\/\///
#> //\\\/\\\\///\\\/\/\\\\/\//\\\\\\/////\\
#> \\/\\\\\////\///\///\//\\\\\\\\\\/\\\\\/
#> /\\/\//////\\\//\/\\/\\\/////\\\\/\\\/\/
#> ////\//\\////\\/////\\/\//\/\/\/\/\///\/
#> \/\\\\///\\///\\/\\//\/\///////\//\////\
#> /\\\//\\////\\\/////\//////\//\//\\\\\//
#> /\\\/\/\\\\\\\/////\////\\\///\/\/\\////
#> \//\//\/\\////\///\//\////\\\\////\\/\\/
#> \/\/\/\\\\/\//\\//\///////////\\/\/\\\\\
#> \////\\/\\//\\\/\//\\//\/\\/\//\\\/\\\\\
#> \/\/\\////\/\//\/\///\\//////\/\/\\/\\\/
#> /\/\\/\\\//\\\/\/\//////\/\//\///\/\/\//
#> \/\/\///\/\//\\\/\/\//\/\/\///\\//\/\\/\
#> \\/\\\/////\////\/\\//\/\//\/\//////\/\\
#> \\\/\/\/\/\/\\//\\//\\//\\/\\/\\/\\\\/\/
#> //\\/\/\\//\/\\/\/\/\\\/\//\\//////\\\/\
where withr::with_options() lets us temporarily
change the print width and cat() concatenates the slashes
and prints out the characters as text.
We can also make this much prettier by drawing the patterns using ggplot2.
Drawing line segments with ggplot2
Instead of writing out slashes, we will draw a grid of diagonal line
segments, some of which will be flipped at random. To draw a segment, we
need a starting x–y coordinate and an ending x–y coordinate.
geom_segment() will connect the two coordinates
with a line. Here’s a small example where we draw four “slashes”.
library(ggplot2)
library(dplyr)
#>
#> Attaching package: 'dplyr'
#> The following objects are masked from 'package:stats':
#>
#> filter, lag
#> The following objects are masked from 'package:base':
#>
#> intersect, setdiff, setequal, union
data <- tibble::tribble(
~row, ~col, ~x_start, ~x_end, ~y_start, ~y_end,
1, 1, 0, 1, 0, 1,
1, 2, 1, 2, 1, 0, # flipped
2, 1, 0, 1, 1, 2,
2, 2, 1, 2, 1, 2
)
ggplot(data) +
aes(x = x_start, xend = x_end, y = y_start, yend = y_end) +
geom_segment()
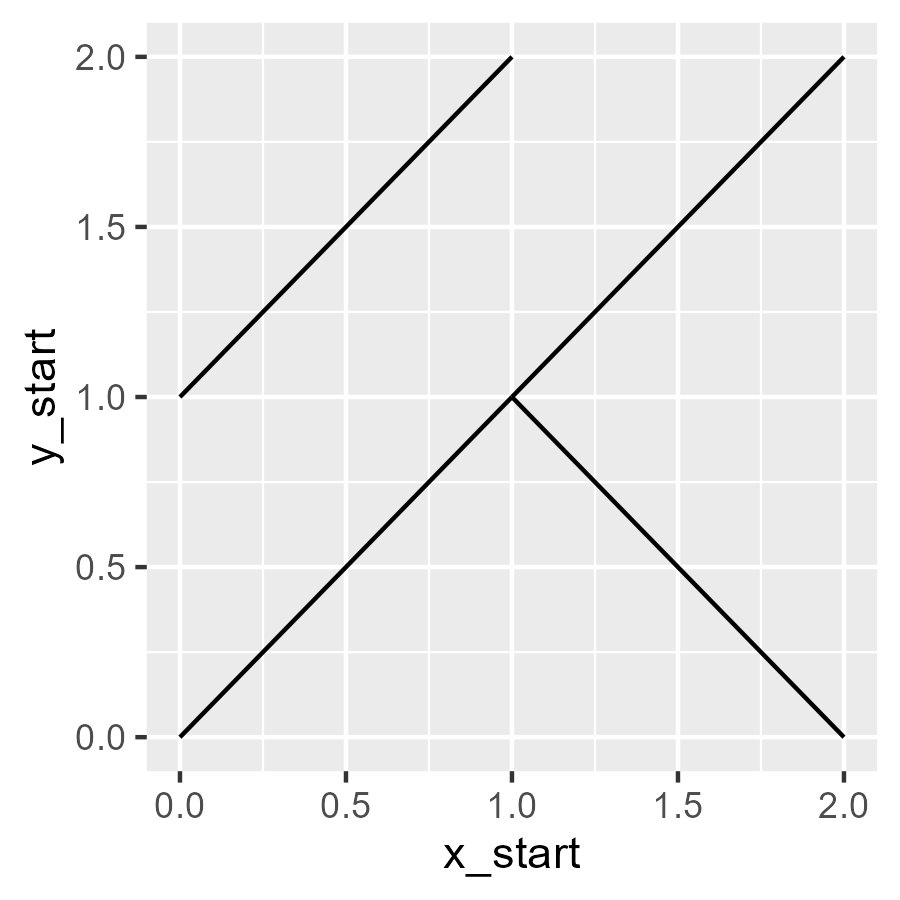
The programming task now is to make giant grid of these slashes. Let’s start with an observation: To draw two slashes, we needed three x values: 0, 1, 2. The first two served as segment starts and the last two as segment ends. The same idea applies to the y values. We can generate a bunch of starts and ends by taking a sequence of steps and removing the first and last elements.
# We want a 20 by 20 grid
rows <- 20
cols <- 20
x_points <- seq(0, 1, length.out = cols + 1)
x_starts <- head(x_points, -1)
x_ends <- tail(x_points, -1)
y_points <- seq(0, 1, length.out = rows + 1)
y_starts <- head(y_points, -1)
y_ends <- tail(y_points, -1)
Each x_starts–x_ends pair is a column in the grid, and each
y_starts–y_ends is a row in the grid. To make a slash at each
row–column combination, we have to map out all the combinations of the
rows and columns. We can do this with crossing() which creates all
crossed combinations of values. (If it helps, you might think of
crossed like crossed
experiments or the
Cartesian cross
product of sets.)
grid <- tidyr::crossing(
# columns
tibble(x_start = x_starts, x_end = x_ends),
# rows
tibble(y_start = y_starts, y_end = y_ends)
) %>%
# So values move left to right, bottom to top
arrange(y_start, y_end)
# 400 rows because 20 rows x 20 columns
grid
#> # A tibble: 400 × 4
#> x_start x_end y_start y_end
#> <dbl> <dbl> <dbl> <dbl>
#> 1 0 0.05 0 0.05
#> 2 0.05 0.1 0 0.05
#> 3 0.1 0.15 0 0.05
#> 4 0.15 0.2 0 0.05
#> 5 0.2 0.25 0 0.05
#> 6 0.25 0.3 0 0.05
#> 7 0.3 0.35 0 0.05
#> 8 0.35 0.4 0 0.05
#> 9 0.4 0.45 0 0.05
#> 10 0.45 0.5 0 0.05
#> # … with 390 more rows
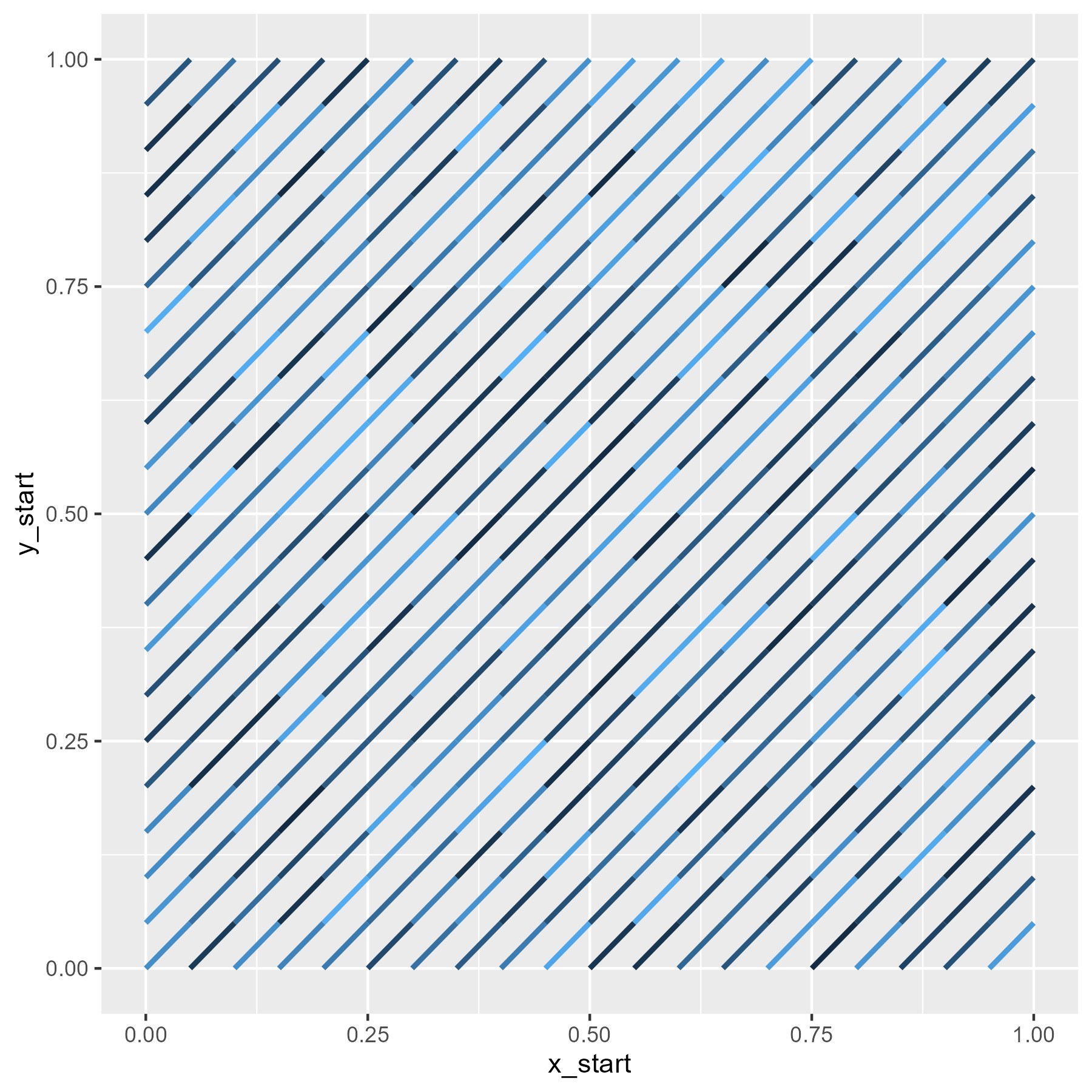
We can confirm that the segments in the grid fill out a plot. (I randomly color the line segments to make individual ones visible.)
ggplot(grid) +
aes(
x = x_start,
y = y_start,
xend = x_end,
yend = y_end,
color = runif(400)
) +
geom_segment(size = 1) +
guides(color = "none")
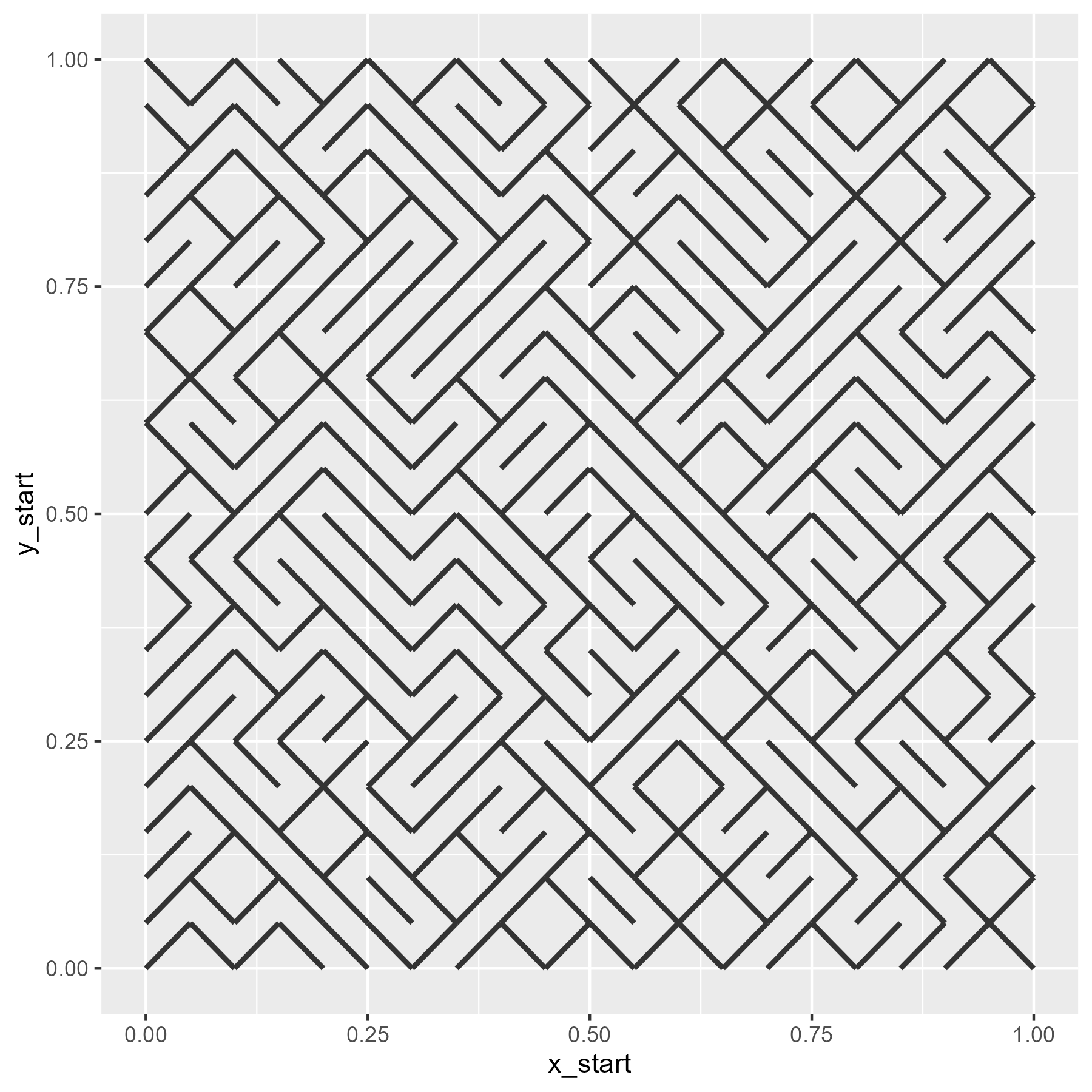
Finally, we need to flip slashes at random. A segment becomes flipped if
the y_start and y_end are swapped. In the code below, we flip the
slash in each row if a randomly drawn number between 0 and 1 is less
than .5. For style, we also use theme_void() to strip away the
plotting theme, leaving us with just the maze design.
p_flip <- .5
grid <- grid %>%
arrange(y_start, y_end) %>%
mutate(
p_flip = p_flip,
flip = runif(length(y_end)) <= p_flip,
y_temp1 = y_start,
y_temp2 = y_end,
y_start = ifelse(flip, y_temp2, y_temp1),
y_end = ifelse(flip, y_temp1, y_temp2)
) %>%
select(x_start:y_end, p_flip)
ggplot(grid) +
aes(x = x_start, y = y_start, xend = x_end, yend = y_end) +
geom_segment(size = 1, color = "grey20")
last_plot() + theme_void()

Now, we wrap all these steps together into a pair of functions.
make_10_print_data <- function(rows = 20, cols = 20, p_flip = .5) {
x_points <- seq(0, 1, length.out = cols + 1)
x_starts <- head(x_points, -1)
x_ends <- tail(x_points, -1)
y_points <- seq(0, 1, length.out = rows + 1)
y_starts <- head(y_points, -1)
y_ends <- tail(y_points, -1)
grid <- tidyr::crossing(
data.frame(x_start = x_starts, x_end = x_ends),
data.frame(y_start = y_starts, y_end = y_ends)
)
grid %>%
arrange(y_start, y_end) %>%
mutate(
p_flip = p_flip,
flip = runif(length(y_end)) <= p_flip,
y_temp1 = y_start,
y_temp2 = y_end,
y_start = ifelse(flip, y_temp2, y_temp1),
y_end = ifelse(flip, y_temp1, y_temp2)
) %>%
select(x_start:y_end, p_flip)
}
draw_10_print <- function(rows = 20, cols = 20, p_flip = .5) {
grid <- make_10_print_data(
rows = rows,
cols = cols,
p_flip = p_flip
)
ggplot(grid) +
aes(x = x_start, y = y_start, xend = x_end, yend = y_end) +
geom_segment(size = 1, color = "grey20")
}
Now the fun part: custom flipping probabilities
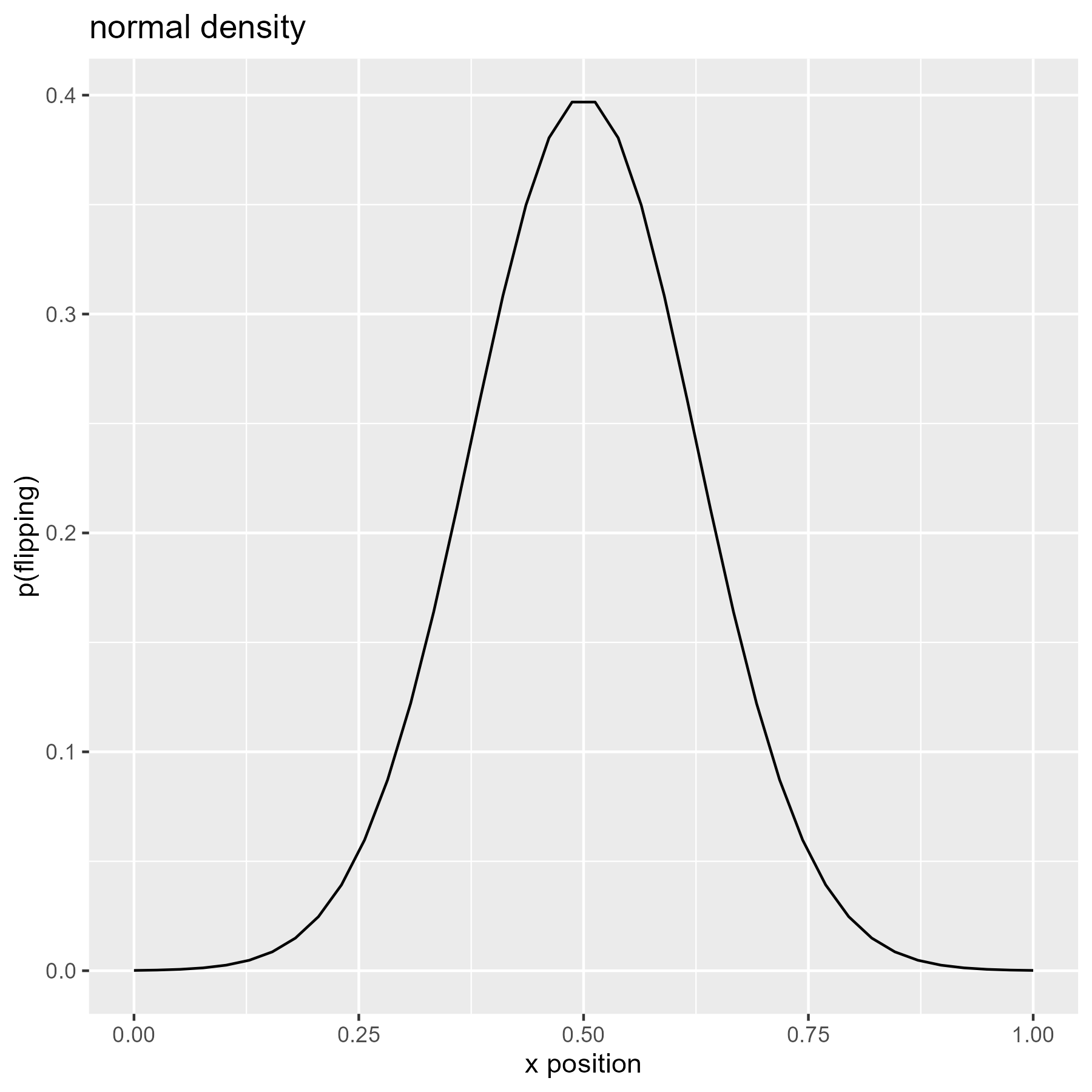
We can vary the probability of flipping the slashes. For example, we can use the density of a normal distribution to make flipping more likely for central values and less likely for more extreme values.
xs <- seq(0, 1, length.out = 40)
p_flip <- dnorm(seq(-4, 4, length.out = 40))
ggplot(data.frame(x = xs, y = p_flip)) +
aes(x, y) +
geom_line() +
labs(
x = "x position",
y = "p(flipping)",
title = "normal density"
)
# We repeat p_flip for each row of the grid
draw_10_print(rows = 40, cols = 40, p_flip = rep(p_flip, 40)) +
theme_void()

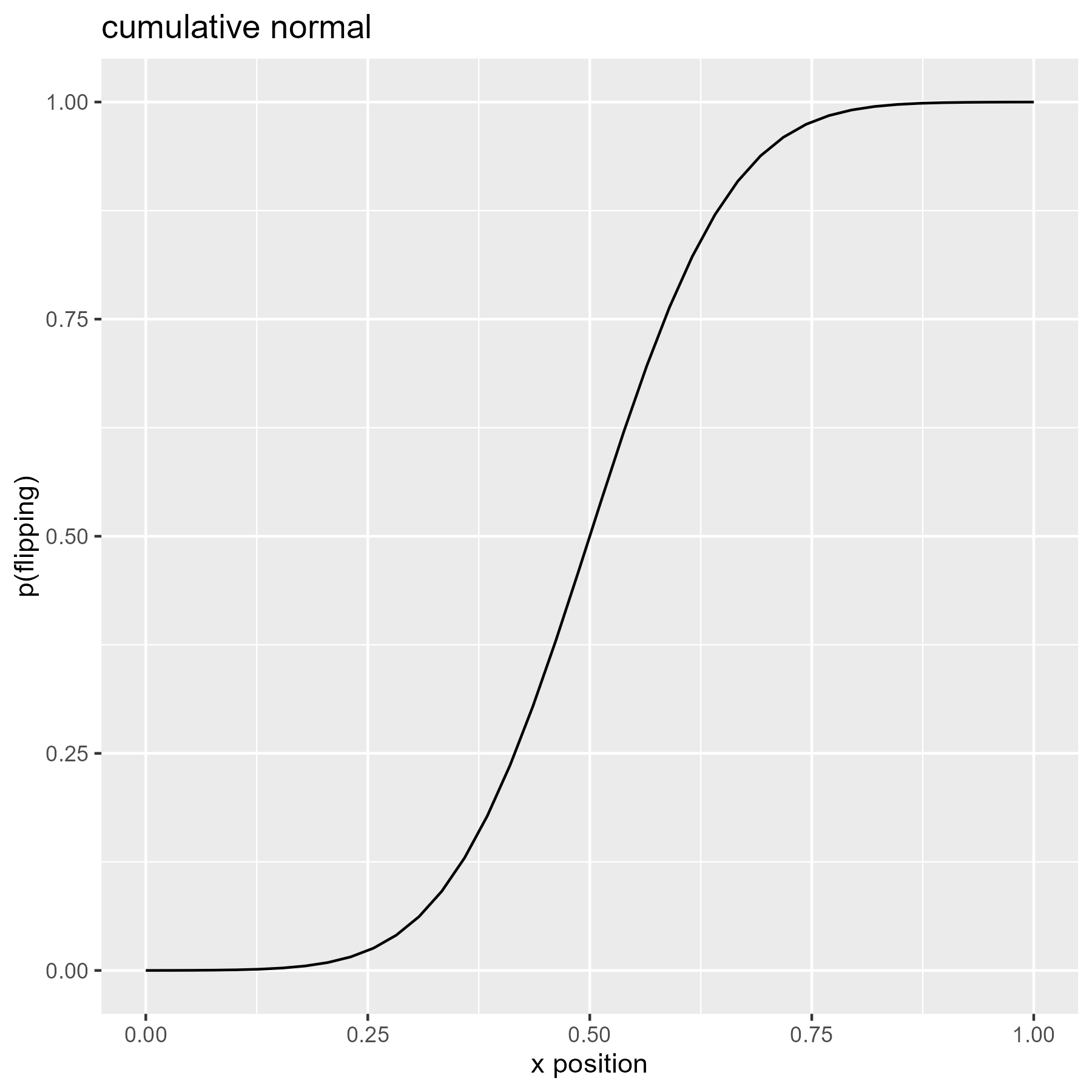
We can use the cumulative density of the normal distribution so that flipping becomes more likely as x increases.
xs <- seq(0, 1, length.out = 40)
p_flip <- pnorm(seq(-4, 4, length.out = 40))
ggplot(data.frame(x = xs, y = p_flip)) +
aes(x, y) +
geom_line() +
labs(
x = "x position",
y = "p(flipping)",
title = "cumulative normal"
)
draw_10_print(rows = 40, cols = 40, p_flip = rep(p_flip, 40)) +
theme_void()

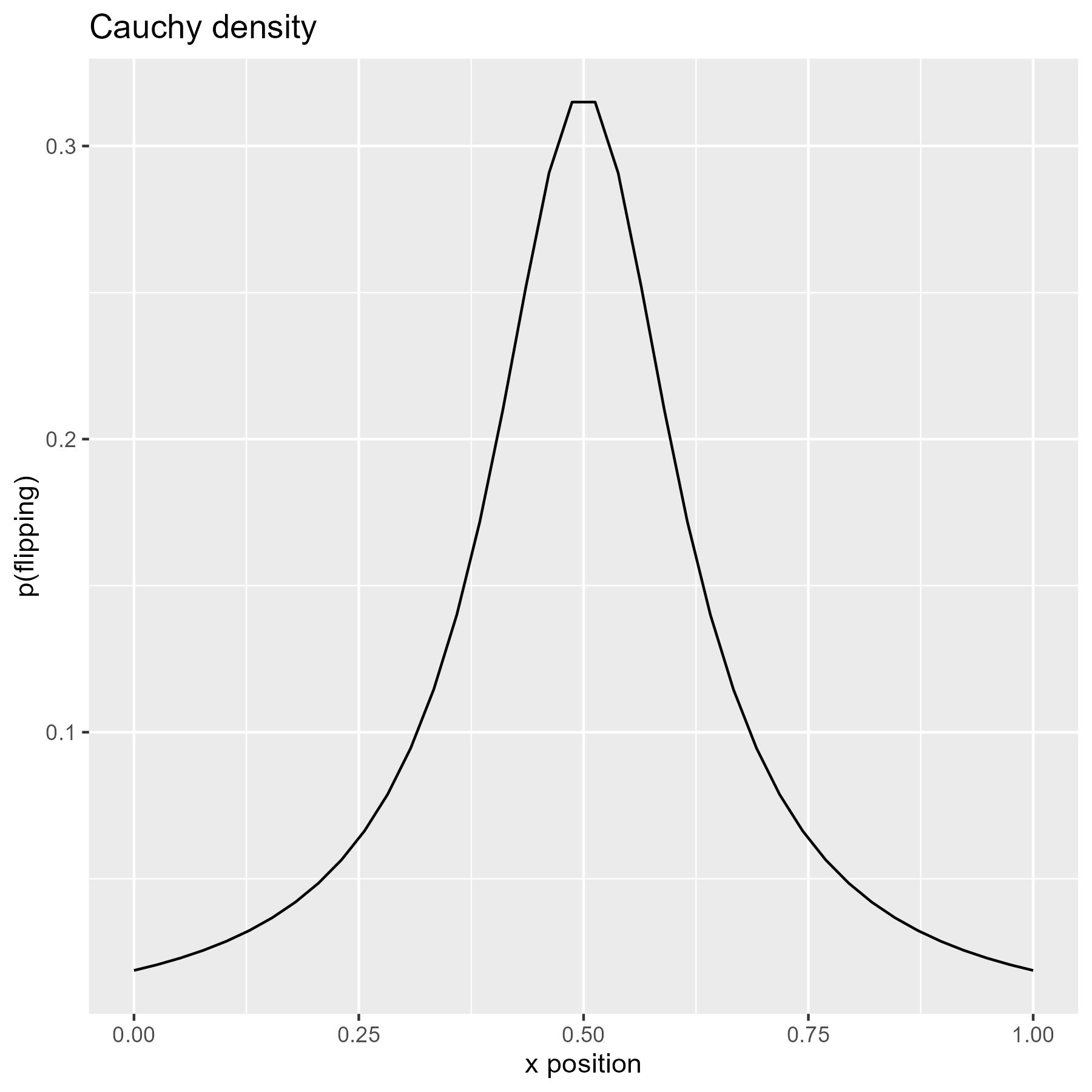
The Cauchy distribution is said to have “thicker” tails than the normal distribution, so here it shows more flips on the left and right extremes.
xs <- seq(0, 1, length.out = 40)
p_flip <- dcauchy(seq(-4, 4, length.out = 40))
ggplot(data.frame(x = xs, y = p_flip)) +
aes(x, y) +
geom_line() +
labs(
x = "x position",
y = "p(flipping)",
title = "Cauchy density"
)
draw_10_print(rows = 40, cols = 40, p_flip = rep(p_flip, 40)) +
theme_void()

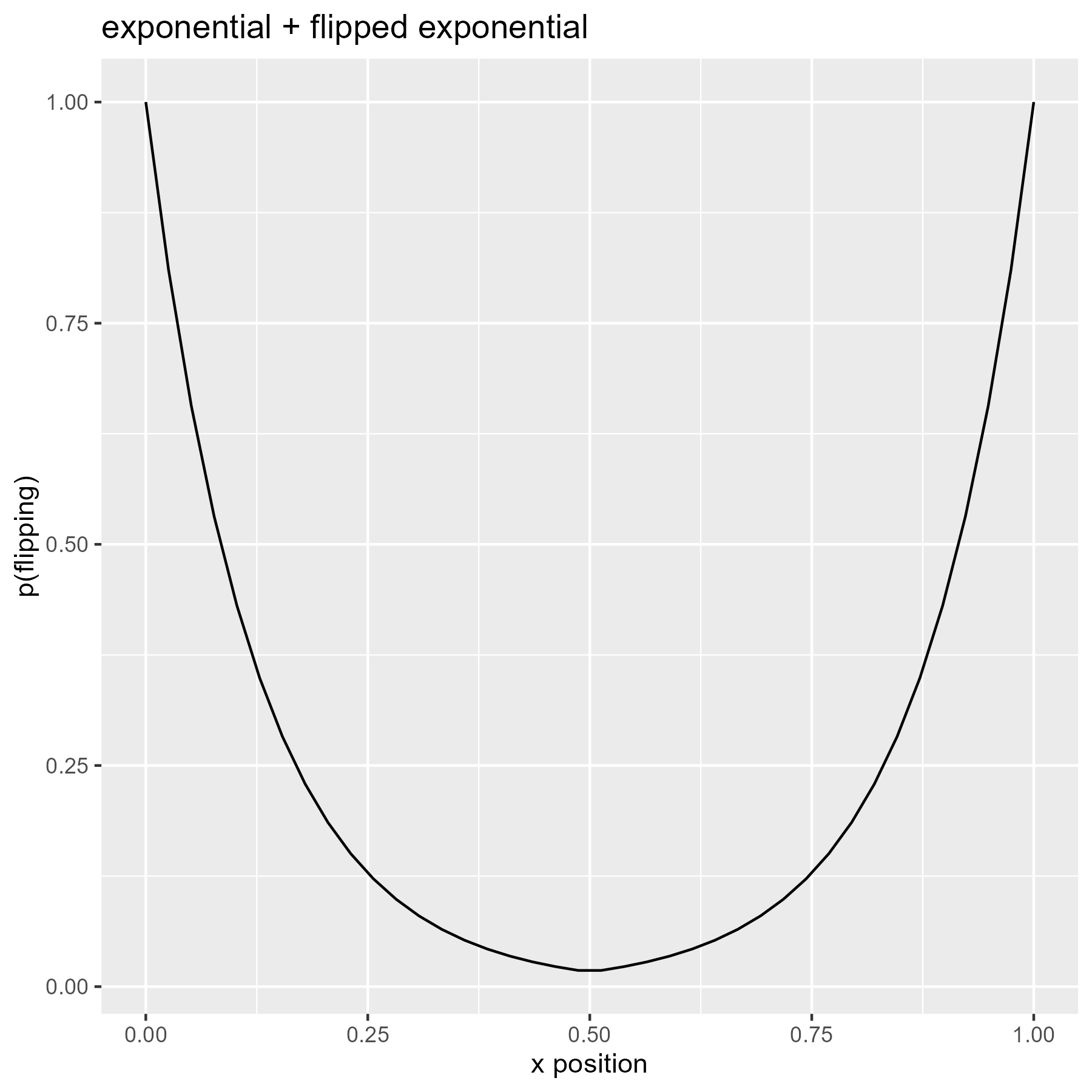
The exponential distribution is a spike that quickly peters out. We can make a probability “bowl” by splicing an exponential and a reversed exponential together.
# Use flipped exponential densities as probabilities
p_flip <- c(
dexp(seq(0, 4, length.out = 20)),
dexp(seq(4, 0, length.out = 20))
)
ggplot(data.frame(x = xs, y = p_flip)) +
aes(x, y) +
geom_line() +
labs(
x = "x position",
y = "p(flipping)",
title = "exponential + flipped exponential"
)
draw_10_print(rows = 40, cols = 40, p = rep(p_flip, 40)) +
theme_void()

We might have the probabilities increase by 10% from row to row. In the code below, I use a simple loop to boost some random probability values by 10% from row to row. This gives us nice streaks in the grid as a column starts to flip for every row.
boost_probs <- function(p_flip, nrows, factor = 1.1) {
output <- p_flip
for (i in seq_len(nrows - 1)) {
p_flip <- p_flip * factor
output <- c(output, p_flip)
}
output
}
draw_10_print(
cols = 40,
rows = 40,
p = boost_probs(runif(40), 40, 1.1)
) +
theme_void()

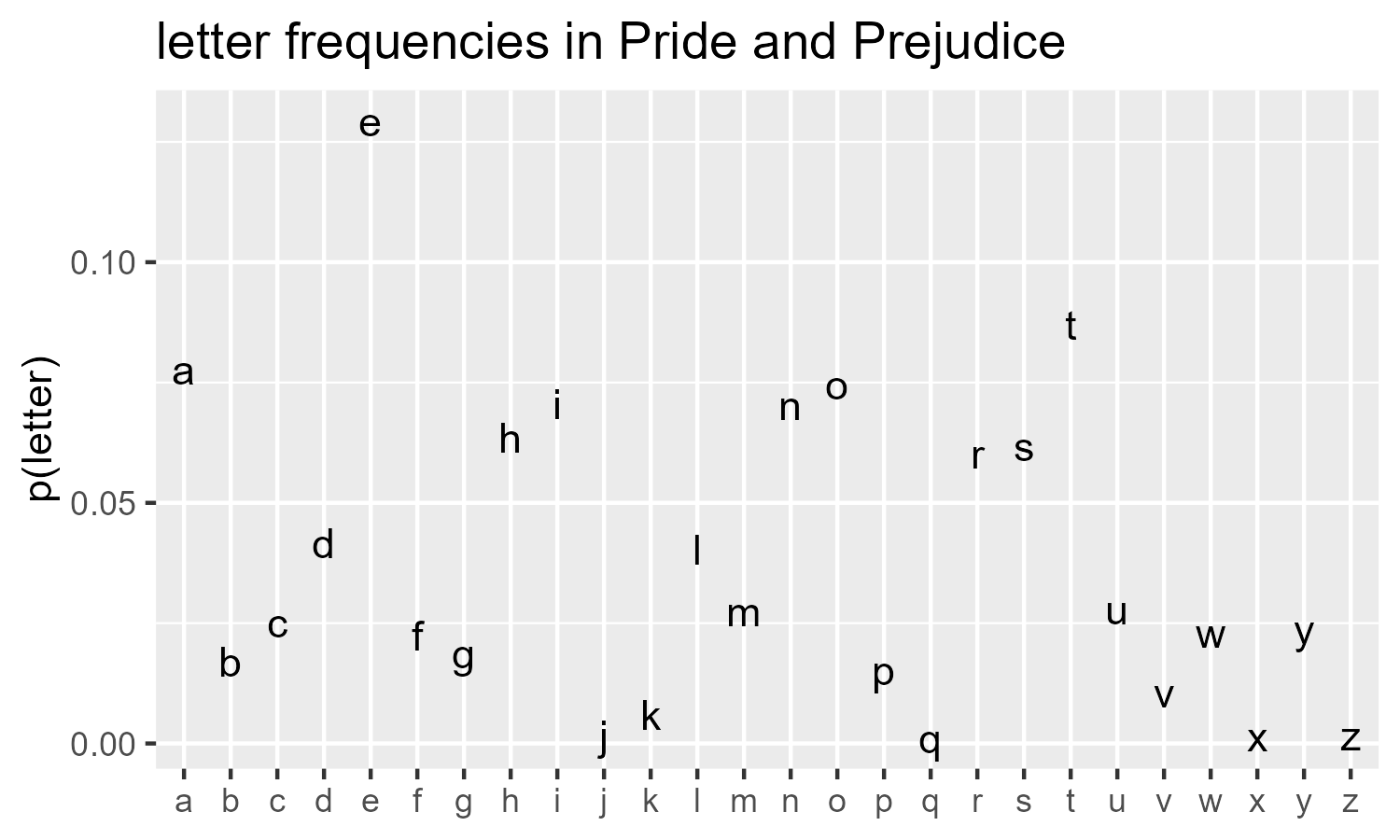
The probabilities can be anything we like. Here I compute the frequency of English alphabet letters as they appear in Pride and Prejudice and based the flipping probability on those values.
char_counts <- janeaustenr::prideprejudice %>%
tolower() %>%
stringr::str_split("") %>%
unlist() %>%
table()
letter_counts <- char_counts[letters] %>% as.vector()
p_letter <- letter_counts / sum(letter_counts)
ggplot(data.frame(x = letters, y = p_letter)) +
aes(x, y, label = x) +
geom_text() +
labs(
x = NULL,
y = "p(letter)",
title = "letter frequencies in Pride and Prejudice"
)
draw_10_print(cols = 26, rows = 80, p = rep(p_letter, 80)) +
theme_void()

Last knitted on 2022-05-27. Source code on GitHub.1
-
.session_info #> ─ Session info ─────────────────────────────────────────────────────────────── #> setting value #> version R version 4.2.0 (2022-04-22 ucrt) #> os Windows 10 x64 (build 22000) #> system x86_64, mingw32 #> ui RTerm #> language (EN) #> collate English_United States.utf8 #> ctype English_United States.utf8 #> tz America/Chicago #> date 2022-05-27 #> pandoc NA #> #> ─ Packages ─────────────────────────────────────────────────────────────────── #> package * version date (UTC) lib source #> assertthat 0.2.1 2019-03-21 [1] CRAN (R 4.2.0) #> cli 3.3.0 2022-04-25 [1] CRAN (R 4.2.0) #> colorspace 2.0-3 2022-02-21 [1] CRAN (R 4.2.0) #> crayon 1.5.1 2022-03-26 [1] CRAN (R 4.2.0) #> DBI 1.1.2 2021-12-20 [1] CRAN (R 4.2.0) #> digest 0.6.29 2021-12-01 [1] CRAN (R 4.2.0) #> dplyr * 1.0.9 2022-04-28 [1] CRAN (R 4.2.0) #> ellipsis 0.3.2 2021-04-29 [1] CRAN (R 4.2.0) #> evaluate 0.15 2022-02-18 [1] CRAN (R 4.2.0) #> fansi 1.0.3 2022-03-24 [1] CRAN (R 4.2.0) #> farver 2.1.0 2021-02-28 [1] CRAN (R 4.2.0) #> generics 0.1.2 2022-01-31 [1] CRAN (R 4.2.0) #> ggplot2 * 3.3.6 2022-05-03 [1] CRAN (R 4.2.0) #> git2r 0.30.1 2022-03-16 [1] CRAN (R 4.2.0) #> glue 1.6.2 2022-02-24 [1] CRAN (R 4.2.0) #> gtable 0.3.0 2019-03-25 [1] CRAN (R 4.2.0) #> here 1.0.1 2020-12-13 [1] CRAN (R 4.2.0) #> highr 0.9 2021-04-16 [1] CRAN (R 4.2.0) #> janeaustenr 0.1.5 2017-06-10 [1] CRAN (R 4.2.0) #> knitr * 1.39 2022-04-26 [1] CRAN (R 4.2.0) #> labeling 0.4.2 2020-10-20 [1] CRAN (R 4.2.0) #> lifecycle 1.0.1 2021-09-24 [1] CRAN (R 4.2.0) #> magrittr 2.0.3 2022-03-30 [1] CRAN (R 4.2.0) #> munsell 0.5.0 2018-06-12 [1] CRAN (R 4.2.0) #> pillar 1.7.0 2022-02-01 [1] CRAN (R 4.2.0) #> pkgconfig 2.0.3 2019-09-22 [1] CRAN (R 4.2.0) #> purrr 0.3.4 2020-04-17 [1] CRAN (R 4.2.0) #> R6 2.5.1 2021-08-19 [1] CRAN (R 4.2.0) #> ragg 1.2.2 2022-02-21 [1] CRAN (R 4.2.0) #> rlang 1.0.2 2022-03-04 [1] CRAN (R 4.2.0) #> rprojroot 2.0.3 2022-04-02 [1] CRAN (R 4.2.0) #> rstudioapi 0.13 2020-11-12 [1] CRAN (R 4.2.0) #> scales 1.2.0 2022-04-13 [1] CRAN (R 4.2.0) #> sessioninfo 1.2.2 2021-12-06 [1] CRAN (R 4.2.0) #> stringi 1.7.6 2021-11-29 [1] CRAN (R 4.2.0) #> stringr 1.4.0 2019-02-10 [1] CRAN (R 4.2.0) #> systemfonts 1.0.4 2022-02-11 [1] CRAN (R 4.2.0) #> textshaping 0.3.6 2021-10-13 [1] CRAN (R 4.2.0) #> tibble 3.1.7 2022-05-03 [1] CRAN (R 4.2.0) #> tidyr 1.2.0 2022-02-01 [1] CRAN (R 4.2.0) #> tidyselect 1.1.2 2022-02-21 [1] CRAN (R 4.2.0) #> utf8 1.2.2 2021-07-24 [1] CRAN (R 4.2.0) #> vctrs 0.4.1 2022-04-13 [1] CRAN (R 4.2.0) #> withr 2.5.0 2022-03-03 [1] CRAN (R 4.2.0) #> xfun 0.31 2022-05-10 [1] CRAN (R 4.2.0) #> #> [1] C:/Users/Tristan/AppData/Local/R/win-library/4.2 #> [2] C:/Program Files/R/R-4.2.0/library #> #> ──────────────────────────────────────────────────────────────────────────────

Leave a comment